JE6: Solving Maxwell equations with wave-propagation and FDTD schemes
In this note I compare solutions for Maxwell equations obtained with the wave-propagation scheme and Finite-Difference Time Domain (FDTD) scheme. These schemes actually solve different forms of the equations and with different layout of the electromagnetic fields on the grid. The wave-propagation scheme collocates all field components while the FDTD scheme staggers the field components on the cell faces and edges. The advantage of the collocated fields is that limiters can be applied that allow the solver to be used when the fields have discontinuities or sharp gradients. The staggered field formulation, on the other hand, satisfies basic vector identities for the discrete fields. This is specially important for the Maxwell equations in which the divergence relations on electric and magnetic fields are not explicitly used in the update equations. However, the staggered field formulation is harder to extend to non-rectangular grids.
One of the intended applications of these Maxwell solvers is to the solution of two-fluid equations. It is straightforward to apply the wave-propagation Maxwell scheme to solve the two-fluid equations. However, some work is required to make the FDTD scheme work with the cell-centered fluid solvers, in particular, the staggered fields need to be interpolated back to cell centers before computing the Lorentz force.
Divergence cleaning in the wave-propagation scheme
The wave-propagation scheme needs electric and magnetic field divergence cleaning. Without this cleaning the solution may be completely incorrect. The perfectly-hyperbolic formulation of the Maxwell equations are used in all the simulations shown here. See this document for the equations used. For all simulations \(\gamma = \chi = 1\), i.e. the errors are propagated at the speed of light.
Problem 1: 2D Transverse Magnetic modes in a box
In this problem the domain is a rectangular metal box \([0, X] \times [0, Y]\). The electric field is initialized with
where \(a = m\pi/X\) and \(b = n\pi/Y\). All other field components are set to zero. Also, \(E_0 = 1\), \(m=8\), \(n=5\), \(X = 80\) and \(Y=40\). All quantities are in SI units. The simulation is evolved to 150 ns. The exact solution for \(E_z\) is
where the frequency \(\omega = c \sqrt{a^2 + b^2}\) and \(c\) is the speed of light.
The first set of simulations were performed to test the convergence of the schemes. The simulations were run on grids \(80 \times 40\), \(160 \times 80\), \(240 \times 120\) and \(320 \times 160\). The time-step was selected to satisfy the CFL condition for that grid resolution. This does not check the convergence of just the spatial discretization (for which we would have to use the same time-step for all grids) but of both the temporal and spatial discretization. For each scheme the error was computed as the average error in \(E_z\) at two time slices, 75 ns and 150 ns.
where \(\hat{E}_z\) is the numerical solution and \(N_x \times N_y\) is the grid size. The summation is performed over all cells.
Convergence of the wave-propagation scheme
The following table shows the errors and order of convergence of the wave-propagation scheme at \(t=75\) ns.
Grid size \(\Delta x\) |
Average error |
Order |
Simulation |
|---|---|---|---|
\(1.00\) |
\(5.4325\times 10^{-2}\) |
||
\(0.50\) |
\(1.3455\times 10^{-2}\) |
\(2.01\) |
|
\(0.3\overline{3}\) |
\(5.9281\times 10^{-3}\) |
\(2.02\) |
|
\(0.25\) |
\(3.3175\times 10^{-3}\) |
\(2.01\) |
The following table shows the errors and order of convergence of the wave-propagation scheme at \(t=150\) ns.
Grid size \(\Delta x\) |
Average error |
Order |
Simulation |
|---|---|---|---|
\(1.00\) |
\(3.2705\times 10^{-2}\) |
||
\(0.50\) |
\(1.3102\times 10^{-2}\) |
\(1.32\) |
|
\(0.3\overline{3}\) |
\(6.3531\times 10^{-3}\) |
\(1.79\) |
|
\(0.25\) |
\(3.7010\times 10^{-3}\) |
\(1.88\) |
It seems a bit odd that the late time solution converges slower than the second-order convergence seen earlier in time. This is probably because phase error in the waves accumulates, reducing the accuracy of the solution.
The following figure shows the wave-propagation solution at \(t=75\) ns.
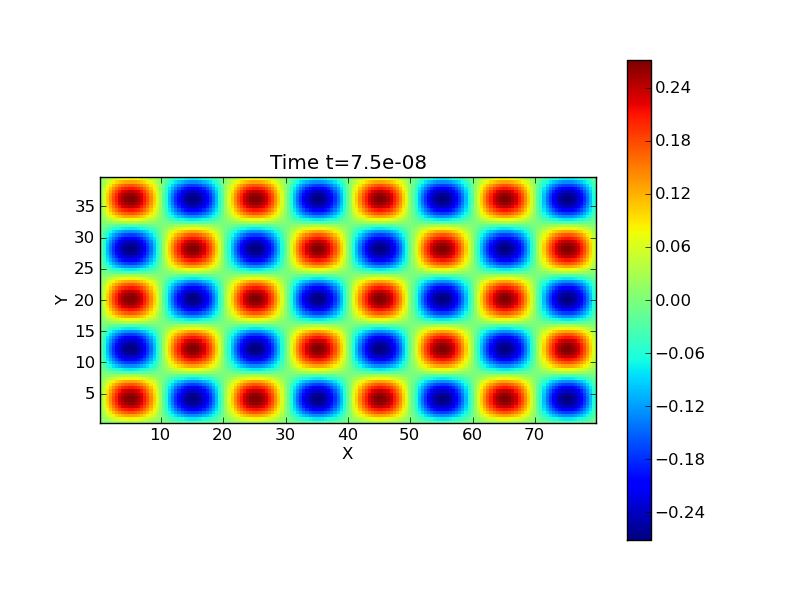
Solution computed with the wave-propagation scheme for \(E_z\) at \(t=75\) ns for \(160 \times 80\) cells [s50].
Convergence of the FDTD scheme
The FDTD scheme requires the electric field at \(t=0\) as well as the magnetic field at \(t=\Delta t/2\). Although in general the exact magnetic field is not available at \(t=\Delta t/2\), it can be computed by using the curl updater and a forward difference in time. If this is not done (i.e. the magnetic field is just initialized at \(t=0\)) the overall scheme becomes first-order. The simulations performed with Lucee use this technique to initialize the simulation.
The following table shows the errors and order of convergence of the FDTD scheme at \(t=75\) ns.
Grid size \(\Delta x\) |
Average error |
Order |
Simulation |
|---|---|---|---|
\(1.00\) |
\(1.4680\times 10^{-2}\) |
||
\(0.50\) |
\(3.7292\times 10^{-3}\) |
\(1.98\) |
|
\(0.3\overline{3}\) |
\(1.6707\times 10^{-3}\) |
\(1.98\) |
|
\(0.25\) |
\(9.4569\times 10^{-4}\) |
\(1.98\) |
The following table shows the errors and order of convergence of the FDTD scheme at \(t=150\) ns.
Grid size \(\Delta x\) |
Average error |
Order |
Simulation |
|---|---|---|---|
\(1.00\) |
\(1.6899\times 10^{-2}\) |
||
\(0.50\) |
\(4.4830\times 10^{-3}\) |
\(1.91\) |
|
\(0.3\overline{3}\) |
\(2.0188\times 10^{-3}\) |
\(1.97\) |
|
\(0.25\) |
\(1.1428\times 10^{-3}\) |
\(1.98\) |
The following figure shows the FDTD solution at \(t=75\) ns.
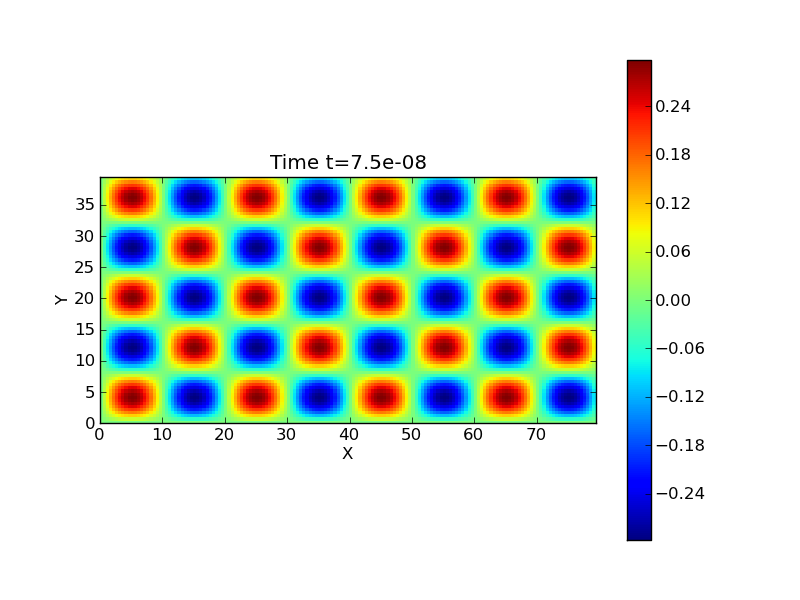
Solution computed with the FDTD scheme for \(E_z\) at \(t=75\) ns for \(160 \times 80\) cells [s54].
Comparison of wave-propagation and FDTD solutions
The following plots compare the solutions obtained by the wave-propagation scheme and the FDTD scheme along the slice \(y=20\) for different grid resolutions.
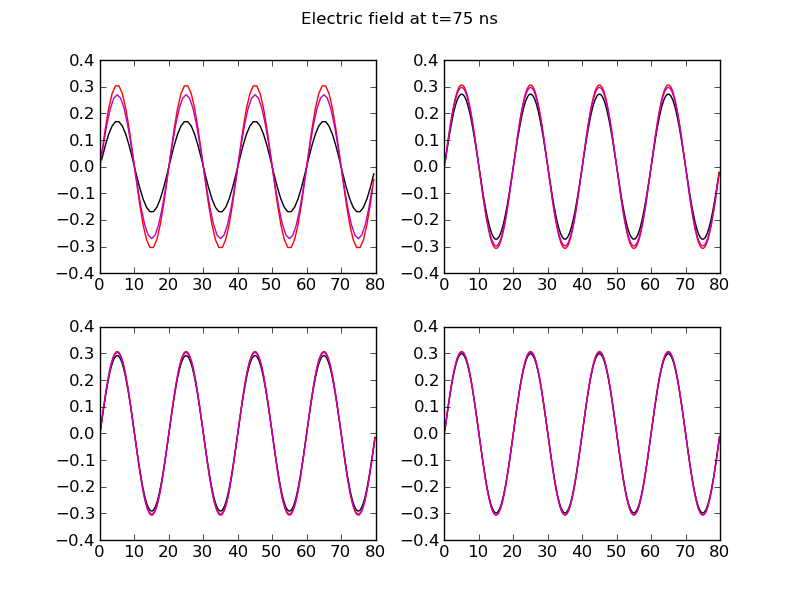
Comparison of wave-propagation solution (black) to FDTD solution (magenta) with exact solution (red) for \(80\times 40\) (top-left), \(160\times 80\) (top-right), \(240\times 120\) (bottom-left) and \(320\times 160\) (bottom-right) at \(t=75\) ns. At lower resolution the FDTD scheme is more accurate but both schemes give good results with higher resolution.
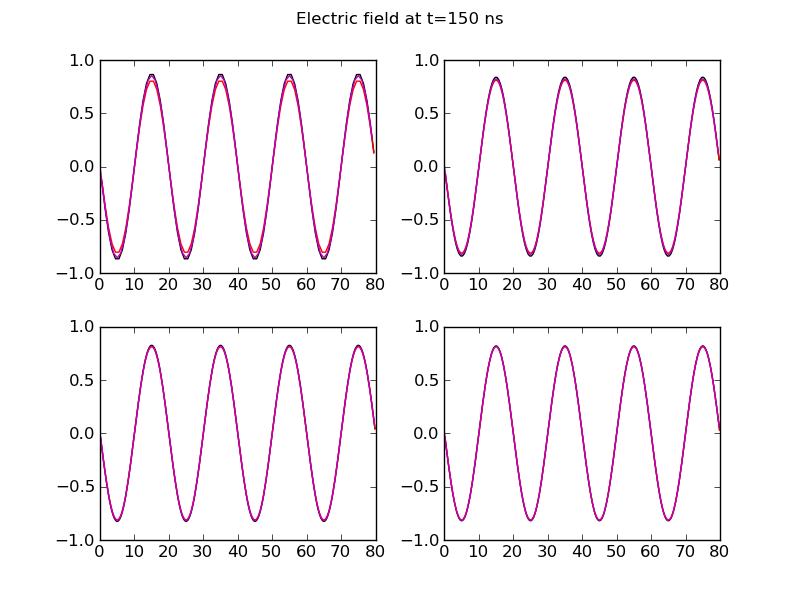
Comparison of wave-propagation solution (black) to FDTD solution (magenta) with exact solution (red) for \(80\times 40\) (top-left), \(160\times 80\) (top-right), \(240\times 120\) (bottom-left) and \(320\times 160\) (bottom-right) at \(t=150\) ns. Both schemes give good results late in time, although the wave-propagation scheme converges slower than the FDTD scheme.
Problem 2: Electromagnetic pulse in a box
In this problem we initialize a Gaussian pulse in a metal box and evolve the resulting fields. The electric field is initialized with
where \(r = \sqrt{x^2 + y^2}\), on a square domain \([-1,1] \times [-1,1]\). Both wave-propagation and FDTD scheme were run on a \(100 \times 100\) grid and \(\beta = 25\). There is no exact solution to this problem and so we use the wave-propagation solution on a \(400 \times 400\) grid as reference. Note that at this higher resolution the wave-propagation and FDTD results are identical to 3 significant digits and so it does not matter which solution is considered “exact”. The FDTD scheme runs 10-15 times faster than the wave-propagation scheme for this problem.
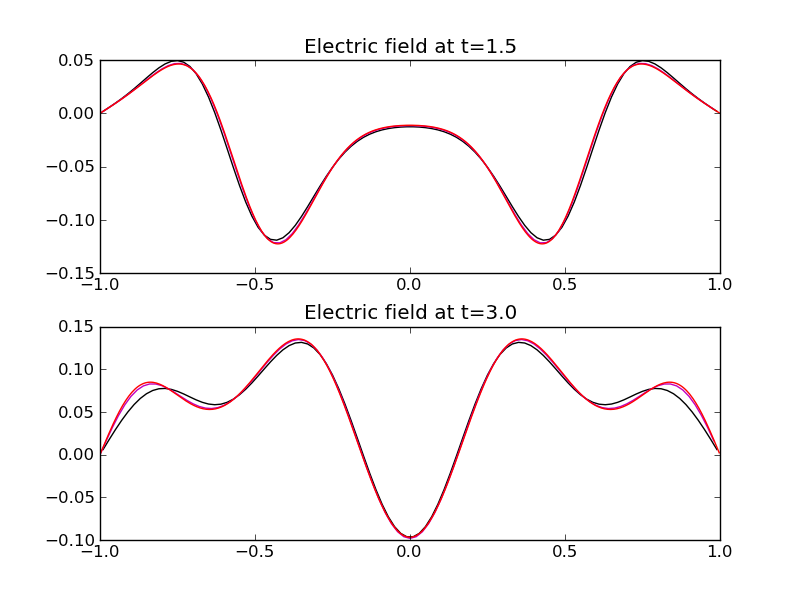
Electric field along the slice \(y=0\) for pulse evolution in a metal box. The wave-propagation solution (black) [s57] is compared to the FDTD solution (magenta) [s58] to the converged solution (red) [s59]. The FDTD runs faster than the wave-propagation scheme and is more accurate.
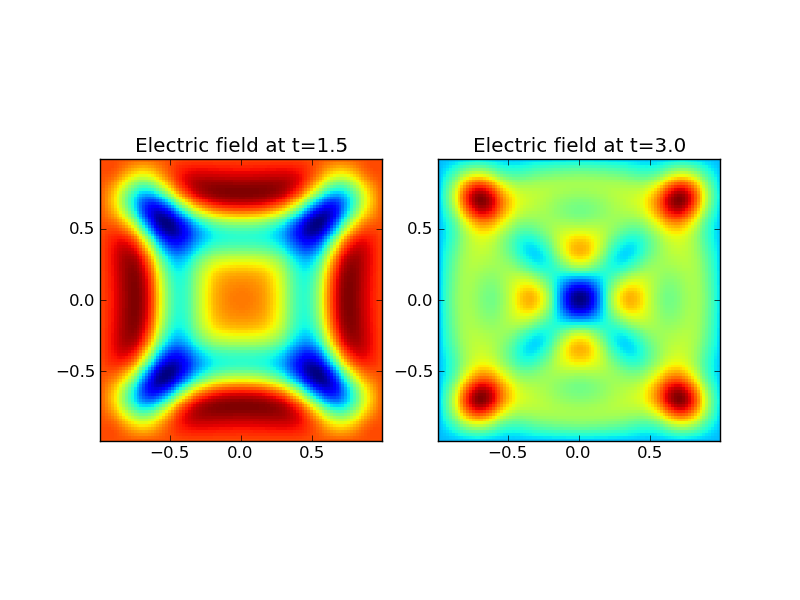
The electric field at \(t=1.5\) (left) and \(t=3.0\) (right) computed from the wave-propagation scheme.
Problem 3: 1D Riemann problem
In this problem the domain is one dimensional, \(0<x<1\), and is initialized with a discontinuity at \(x=0.5\). Open boundary conditions are applied. The initial discontinuity breaks up into a series of discontinuities, which are either stationary or move with the speed of light. The left and right states are
and the simulations are run to \(t=0.25\) on a grid of 100 cells.
As seen in the figure below, the FDTD solution shows severe oscillations caused due to the initial discontinuity in the fields. These oscillations are from the central differencing operator applied across the discontinuity and, due to the lack of diffusion, do not damp out. The wave-propagation scheme, on the other hand, uses a limiting procedure that allows it to capture the solution well.
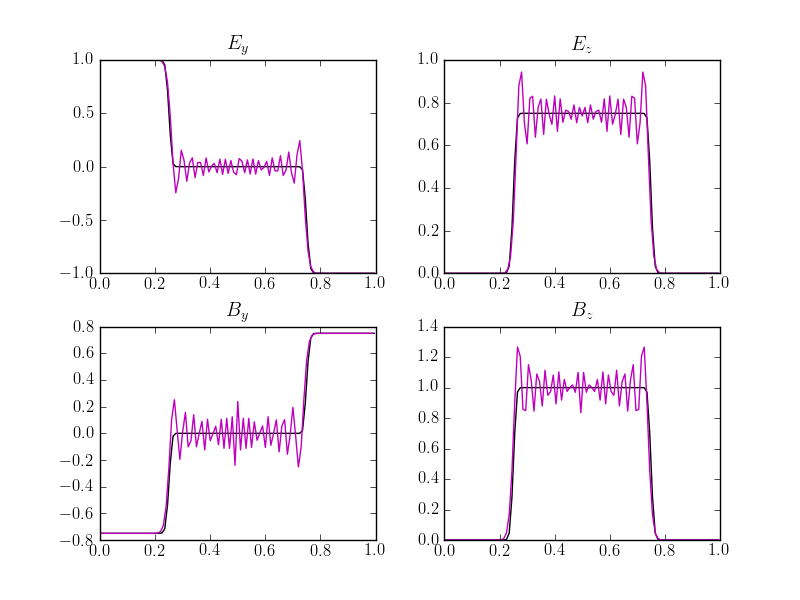
Comparison of the wave-propagation solution (black) [s61] with the FDTD solution (magenta) [s62] at \(t=0.25\). The plots show \(E_y\) (upper left), \(E_z\) (upper right), \(B_y\) (lower left) and \(B_z\) (lower right). The wave-propagation solution is smooth and shows no numerical artifacts, while the FDTD solution shows severe oscillations due to the discontinuities.
Conclusions
From these simulations we can conclude that
The FDTD scheme is more efficient and accurate than the wave-propagation scheme when the fields are smooth. In fact, the FDTD scheme runs 10-15 times faster in 2D. This is not surprising as solving a Riemann problem at each interface makes the wave-propagation scheme slower while upwinding adds diffusion.
The FDTD scheme, by construction, preserves the divergence relations by using staggered fields. On the other hand, the wave-propagation scheme needs some sort of cleaning to maintain the divergence relations.
The wave-propagation scheme can resolve discontinuities and sharp features in the field. The FDTD scheme, on the other hand, adds oscillations around discontinuities. This is generally not an issue as most applications of Maxwell equations have smooth solutions. However, when doing multi-fluid simulations this can be a problem as, in certain situations, the fluids can develop shocks which in turn, due to field-line freezing, can lead to shocks in the field.
The advantage of the wave-propagation (and other co-located field schemes) is that it is easier to extend to non-rectangular grids. It should be possible to develop a hybrid scheme that has best of both these schemes by utilizing the duality property of fluxes in the Riemann solver based schemes and the fields in FDTD scheme.