JE14: A DG scheme for Vlasov equation with fixed potential 

Contents

JE14: A DG scheme for Vlasov equation with fixed potential

In this document I test a discontinuous Galerkin (DG) scheme for the solution of the 1D Vlasov equation written as

\[\frac{\partial f}{\partial t} = \{H,f\}\]

where \(f(x,v,t)\) is the distribution function, \(H(x,v)\) is a Hamiltonian function and where \(\{H,f\}\) is the Poisson bracket operator defined by

\[\{H,f\} = \frac{\partial H}{\partial x}\frac{\partial f}{\partial v} - \frac{\partial H}{\partial v}\frac{\partial f}{\partial x}.\]

The Hamiltonian takes the form 1

\[H = \frac{1}{2}v^2 + \frac{q}{m}\phi\]

where \(\phi(x,t)\) is a scalar potential and \(q\) and \(m\) are the particle charge and mass respectively. In this note the potential is specified and time-independent. For the Vlasov-Poisson system, however, the potential is determined from either a Poisson solve or from the requirements of quasi-neutrality. With this Hamiltonian the Vlasov equation can be written in the familiar form

\[\frac{\partial f}{\partial t} + v\frac{\partial f}{\partial x} - \frac{q}{m}\frac{\partial \phi}{\partial x} \frac{\partial f}{\partial v} = 0.\]

Note

The Lua programs implementing these simulations are quite complicated due to the fact that the moments and potential live on a 1D spatial grid while the distribution function itself lives on a 2D phase-space grid. This means that basis functions, fields and updaters need to be defined on both grids, with additional operators to go between them.

Problem 1: Free streaming 

In the first test we set \(\phi = 0\), which leads to the free-streaming (constant advection) equation

\[\frac{\partial f}{\partial t} + v\frac{\partial f}{\partial x} = 0.\]

Note that the exact solution to this equation is simply

\[f(x,v,t) = f(x-vt,v,0)\]

i.e. for at each point in velocity space the initial distribution advects with a constant speed. However, even though the distribution function is manifestly undamped, its moments are damped. To see this pick an initial condition a Maxwellian 2

\[f(x,v,0) = \frac{1}{\sqrt{2\pi v_t}} \exp(-v^2/2v_t^2) \cos(kx)\]

where \(v_t\) is the thermal velocity and \(k\) is the wave-number. Then, the exact solution is

\[f(x,v,t) = \frac{1}{\sqrt{2\pi v_t}} \exp(-v^2/2vt^2) \cos\left( k(x-vt) \right)\]

The increasingly oscillatory nature of the \(\cos\left( k(x-vt) \right)\) term results in phase mixing due to which all moments of the distribution functions are severely damped. For example, the number density is

\[n(x,t) = \int_{-\infty}^\infty f dv = e^{-k^2v_t^2t^2/2} \cos(kx)\]

which is exponentially damped.

Accuracy test 

To test the ability of the algorithm to model this damping, a simulation is initialized with a Maxwellian with \(v_t=1\) and \(k=1\) on a domain \((x,v) \in [0,2\pi] \times [-6,6]\). The number density is computed and diagnostics inserted to record the time-dependent density in a specified cell.

The results on a \(64\times 64\) grid with DG second order scheme with upwind fluxes are show below.

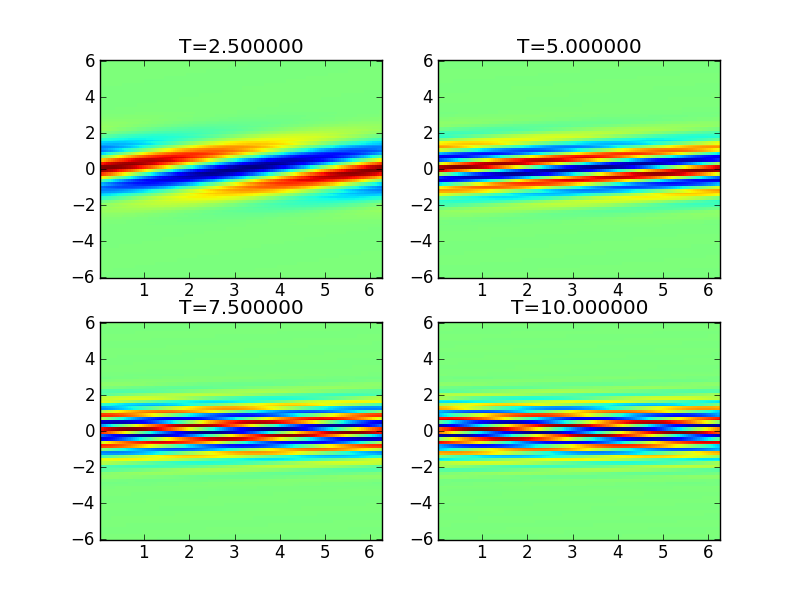
../../_images/s143-vlasov-free-stream_distf.png — Distribution function \(f(x,v,t)\) at different times for free-streaming problem. This simulation [s143] was performed on a \(64\times 64\) grid with DG second order scheme with upwind fluxes. Seen is the increasing striations in the distribution function due to the differential advection at different velocities and the initial spatial perturbation.

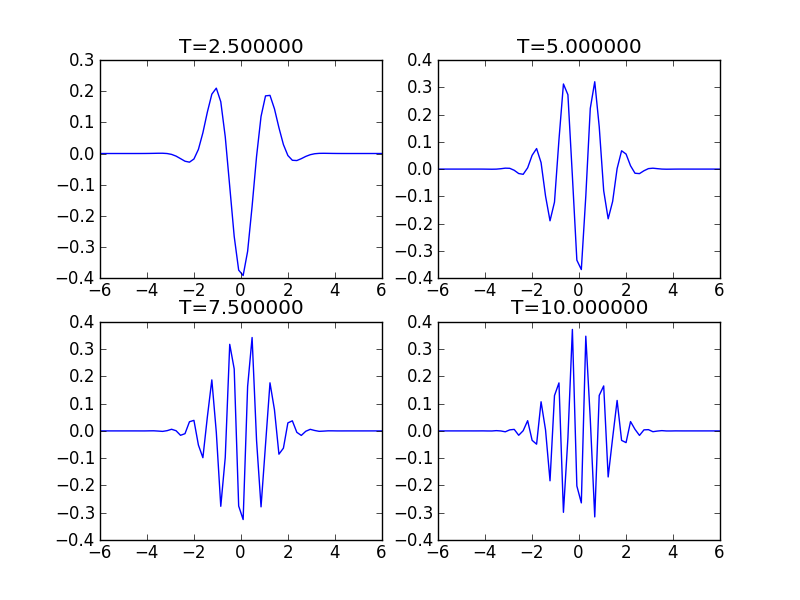
../../_images/s143-vlasov-free-stream_distf_v.png — Distribution function \(f(x=\pi,v,t)\) at different times for free-streaming problem. The increasingly oscillatory nature of the distribution function is evident in this plot. See previous figure caption for other details.

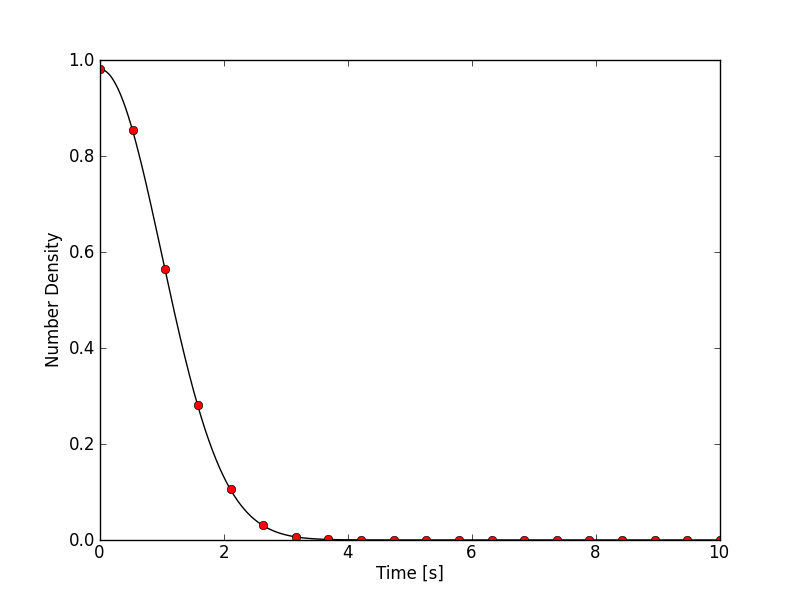
../../_images/s143-vlasov-free-stream_numDensInCell.png — Number density (black) in cell 2 as a function of time. The red dots show the exact solution. For this resolution the numerical solution is indistinguishable from the exact solution. See previous figure caption for other details.

Recurrence phenomena 

The discrete velocity space grid combined with a lack of true physical (or numerical) damping will lead to recurrence, i.e, the initial conditions will recur almost exactly after a finite amount of time. To see this the above simulation was run on a coarser mesh with \(32 \times 8\) and \(32\times 16\) cells with a second and third spatial order scheme. The results are show below.

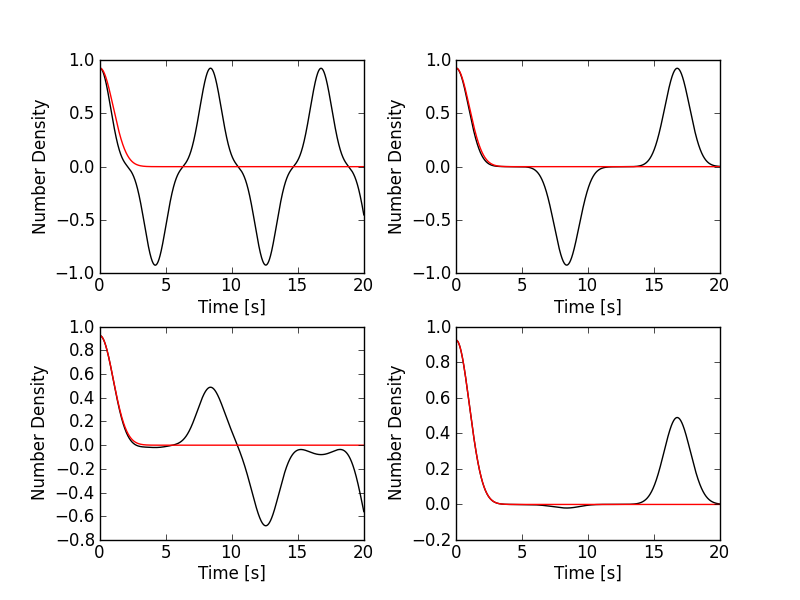
../../_images/s14_4567_-vlasov-free-stream_numDensInCell.png — Number density (black) as a function of time with DG2 on 8 velocity cells [s144] (top left), DG2 on 16 velocity cells [s145] (top right), DG3 on 8 velocity cells [s146] (bottom left) and DG3 on 16 velocity cells [s147] (bottom right). The red line shows the exact solution. The recurrence is clearly visible in the second order scheme, and occurs later as the velocity grid is refined. Exact recurrence in the third-order scheme is not seen on this time-scale.

Problem 2: Particles in a potential well 

In this set of problems the potential was held fixed and the distribution evolved. These cases correspond to the motion of test particles in a specified potential. In each case the initial distribution is assumed to be a uniform Maxwellian

\[f(x,v,0) = \frac{1}{\sqrt{2\pi v_t}} \exp(-v^2/2v_t^2)\]

with \(v_t=1.0\). If the potential has a well (a minima) then a fraction of the particles will be trapped and appear as rotating vortices in the distribution function plots. The bounce period for a particle with energy total \(E\) (which is a constant of motion) in a well can be computed from

\[T(E) = \sqrt{2m} \int_{x_1(E)}^{x_2(E)} \frac{dx}{\sqrt{E-\phi(x)}}\]

where \(x_1\) and \(x_2\) are the roots of the equation \(\phi(x)=E\), i.e. the turning points at which the motion of the particle changes sign. For finite \(x_1\) and \(x_2\) the motion is periodic. Note that for a non-singular distribution (like the Maxwellian) the bounce period need not be the same for all the particles. In this case an average period can be computed.

A \(\cos(x)\) potential well 

In this problem the potential is specified as

\[\phi(x) = \cos(x)\]

Simulations were run with a DG2 scheme on a \(64\times 128\) grid for \((x,v) \in [0,2\pi] \times [-6,6]\).

In this potential the bounce period of a single particle depends on its initial energy. This is seen in the movie in which the particles with smaller total energy bounce faster.

Snapshots are shown at a \(t=3\) and \(t=20\) below.

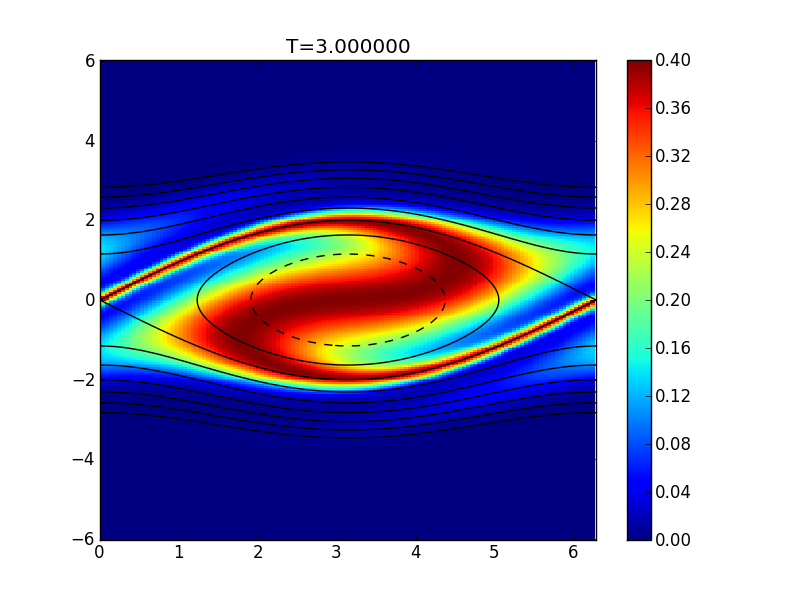
../../_images/s149-vlasov-fp_distf_00015.png — Distribution function at \(t=3\) for flow in a potential well. The black lines show contours of constant particle energy. A separatrix forms along the trapped-passing boundary. Simulation run with a DG2 scheme on a \(64\times 128\) grid [s149].

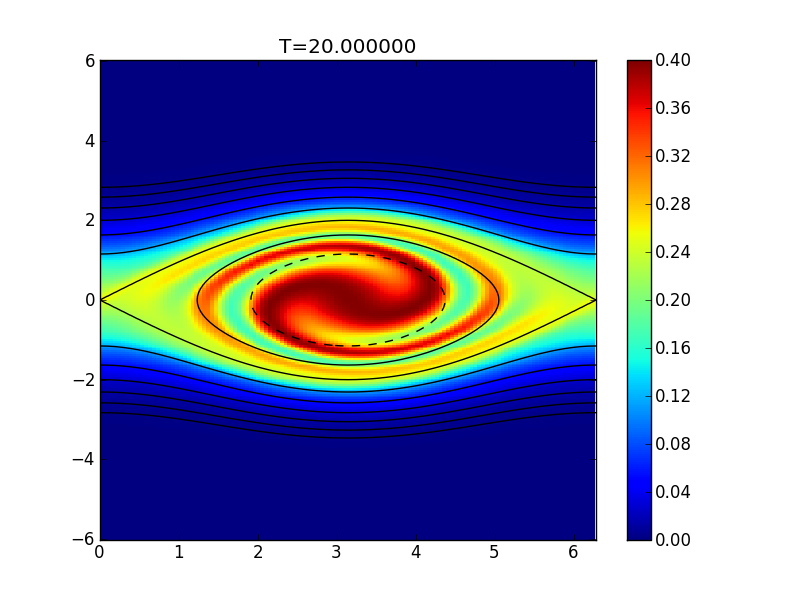
../../_images/s149-vlasov-fp_distf_00100.png — Distribution function at \(t=20\) for flow in a potential well. See previous figure captions for other details.

A quadratic \(\phi(x)=x^2\) potential well 

In this problem the potential is specified as

\[\phi(x) = x^2\]

Simulations were run with a DG2 scheme on a \(64\times 128\) grid for \((x,v) \in [-1,1] \times [-6,6]\). In this potential well the bounce period is the same for all particles and can be computed as \(\pi\sqrt{2} \approx 4.443\). Also, as the bounce period for all trapped particles is the same, these will move “rigidly” in phase space, i.e. the motion along contours of constant energy will occur with the same angular frequency.

These features are clearly seen in the movie which shows the correct bounce period. Also, it is seen that most of the particles are trapped and the distribution function “rotates rigidly” inside the trapped region.

Snapshots are shown at a \(t=3\) and \(t=20\) below.

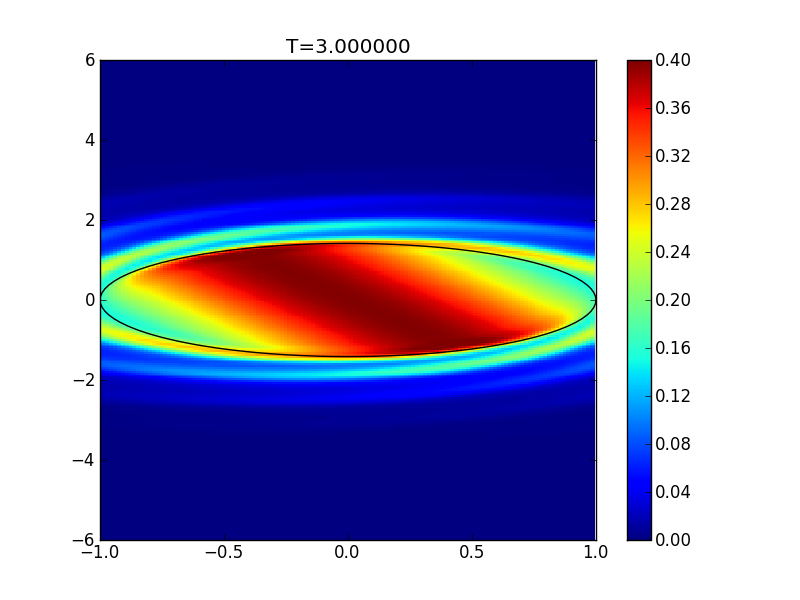
../../_images/s150-vlasov-fp_distf_00015.png — Distribution function at \(t=3\) for flow in a potential well. The black line shows the trapped-passing energy contour. Due to the quadratic potential, all particles inside the trapped region move with the same angular velocity in phase space. Simulation run with a DG2 scheme on a \(64\times 128\) grid [s150].

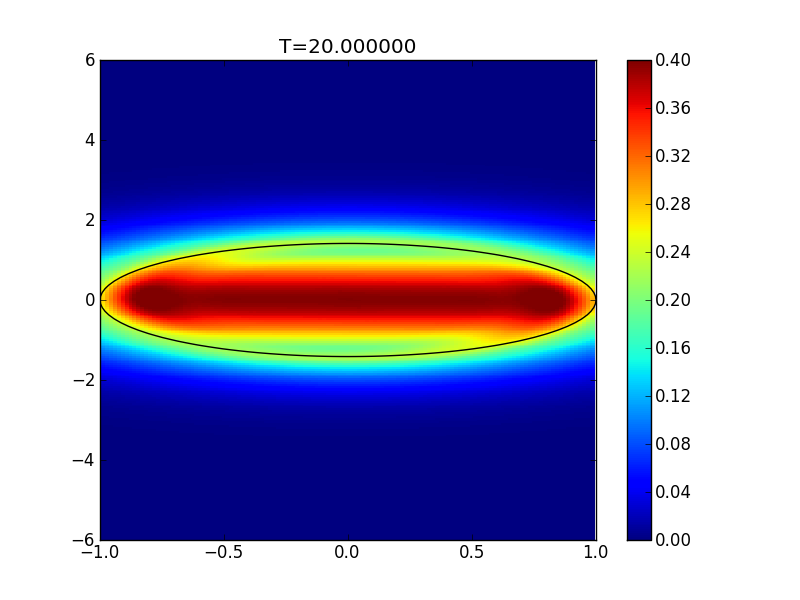
../../_images/s150-vlasov-fp_distf_00100.png — Distribution function at \(t=20\) for flow in a potential well. See previous figure captions for other details.

Conclusions 

The ability of the discontinuous Galerkin Vlasov solver to handle free-streaming and fixed-potential problems is demonstrated. Recurrence is seen to occur due to a lack of true physical or numerical dissipation. The appropriate amount of such dissipation can be provided from (hyper) collisions and this needs to be implemented. One aim of this note was to ensure that all the moment and diagnostic updaters are working correctly. This is slightly tricky as one needs to go between 2D and 1D grids with different basis functions. Everything seems to be working as expected.

1

The Hamilitonian should be written in canonical coordinates as

\[H = \frac{p^2}{2m} + q\phi\]

where \(p=mv\) is the particle momentum. However, for the simple case considered here the two definitions lead to the same dynamical equation for the distribution function.

2

The form of the initial condition means that the distribution function is allowed to go negative. This is okay in this test problem, but for plasmas positivity of the distribution function is a required condition of physical realizability.