JE3: Testing the radiation transport equation solver in a homogeneous slab

Contents

• JE3: Testing the radiation transport equation solver in a homogeneous slab

  • Problem formulation and Fourier decomposition

  • Test Problems and Results

    • Problem 1

    • Problem 2

    • Problem 3

    • Problem 4

  • References

Problem formulation and Fourier decomposition

In this entry I test the solver for the radiation transport equation (RTE) in a homogeneous slab. In addition to stand-alone use this solver can be used as a building block for solving the RTE in an inhomogeneous slab.

Although it might seem that the problem of the RTE in a slab is only of academic interest, it finds applications in understanding the radiation in the Earth’s (and other planetary) atmosphere and oceans. To an excellent approximation the atmosphere and the ocean can be treated as horizontally uniform with optical properties varying only with depth. See, for example, [Mobley1994] and [Thomas1999]. The key difficulty in solving the RTE for such applications is highly anisotropic scattering with a strong forward component. This requires the use of special algorithms to accurately handle the angular dependence of the radiation field.

The systematic study of the RTE was initiated by Subrahmanyan Chandrasekhar. He wrote a now-classic monograph [ChandraRT] (based on a series of his papers) in which he developed very elegant analytical methods to solve the RTE (including the effects of polarization) in homogeneous slabs. Chandra’s book is a tour de force in mathematical physics and has inspired several algorithms now in common use.

The RTE is a linear integro-differential equation and is written as

\[\mu\frac{\partial L(\tau,\mu,\phi)}{\partial \tau} + L(\tau,\mu,\phi) = \frac{\varpi}{4\pi} \int_{-1}^1 \int_0^{2\pi} p(\cos\Theta) L(\tau,\mu,\phi) d\mu d\phi\]

where

• \(L(\tau,\mu,\phi)\) is the radiance in units of Watt \(\mathrm{m}^{-2}\) \(\mathrm{sr}^{-1}\) \(\mathrm{nm}^{-1}\),

• \(0 < \tau < \tau_0\) is the optical depth,

• \(\varpi\) is the albedo of single scattering,

• \(\mu\) is the cosine of the polar angle measured with the positive \(Z\)-axis and \(\phi\) is the azimuthal angle,

• \(p(\cos\Theta) = \sum_{l=0}^L\beta_lP_l(\cos\Theta)\) is the phase function, where \(\Theta\) is the scattering angle and \(\beta_0=1\).

The boundary conditions are a directed beam incident at \(\tau=0\) and a “black” boundary at \(\tau=\tau_0\)

\[\begin{split}&L(0, \mu) = \pi F \delta(\mu-\mu_0) \delta(\phi-\phi_0) \\ &L(\tau_0, -\mu) = 0\end{split}\]

for \(\mu\in [0,1]\), and where

• \(\tau_0\) is the optical depth of the slab,

• \(\mu_0\) and \(\phi_0\) are the cosine of the polar angle and azimuthal angle of incident beam,

• \(\mu_0\pi F\) is the total downward irradiance incident on the slab.

The singular component of the radiance is removed using the decomposition

\[L(\tau,\mu,\phi) = L_*(\tau,\mu,\phi) + \pi F \delta(\mu-\mu_0) \delta(\phi-\phi_0) e^{-\tau/\mu_0}\]

Where \(L_*(\tau,\mu,\phi)\) is the diffuse (scattered at least once) component of the radiance. Further, the addition theorem of spherical harmonics is used to write

\[p(\cos\Theta) = \sum_{m=0}^L(2-\delta_{0,m}) \sum_{l=m}^L\beta_l P_l^m(\mu) P_l^m(\mu') \cos[m(\phi'-\phi)]\]

where

\[P_l^m(\mu) = \left[ \frac{(l-m)!}{(l+m)!} \right]^{1/2} (1-\mu^2)^{1/2}\frac{d^m}{d\mu^m} P_l(\mu)\]

are the normalized Legendre functions. The diffuse radiance is expanded in a Fourier cosine series as

\[L_*(\tau,\mu,\phi) = \frac{1}{2} \sum_{m=0}^L (2-\delta_{0,m})L^m(\tau,\mu) \cos[m(\phi-\phi_0)]\]

Using these definitions the RTE becomes a set of equations for each Fourier component \(L^m(\tau,\mu)\)

\[\mu\frac{\partial L^m(\tau,\mu)}{\partial \tau} + L^m(\tau,\mu) = \frac{\varpi}{2} \sum_{l=m}^L \beta_l P_l^m(\mu) \int_{-1}^1 P_l^m(\mu') L^m(\tau,\mu') d\mu' + Q^m(\tau,\mu)\]

and

\[Q^m(\tau,\mu) = \frac{\varpi F}{2}e^{-\tau/\mu_0} \sum_{l=m}^L \beta_l P^m_l(\mu_0) P_l^m(\mu)\]

The boundary conditions on each Fourier component become

\[\begin{split}&L^m(0, \mu) = 0 \\ &L^m(\tau_0, -\mu) = 0.\end{split}\]

The algorithm implemented in Lucee is described in full detail in a paper by Siewert [Siewert2000].

Test Problems and Results

The test problems solved in this note are taken from [Garcia1985] that also lists very accurate benchmark results for these problem. For each problem the results computed with Lucee are plotted against the tabulated data in Garcia and Siewert.

Problem 1

Mie scattering with \(L=8\) case for slab with \(\tau_0=1\), \(\mu_0 = 0.5\) and \(\varpi=0.95\).

Lucee results are compared to Garcia and Siewert results for Fourier modes \(m=0\) and \(m=1\).

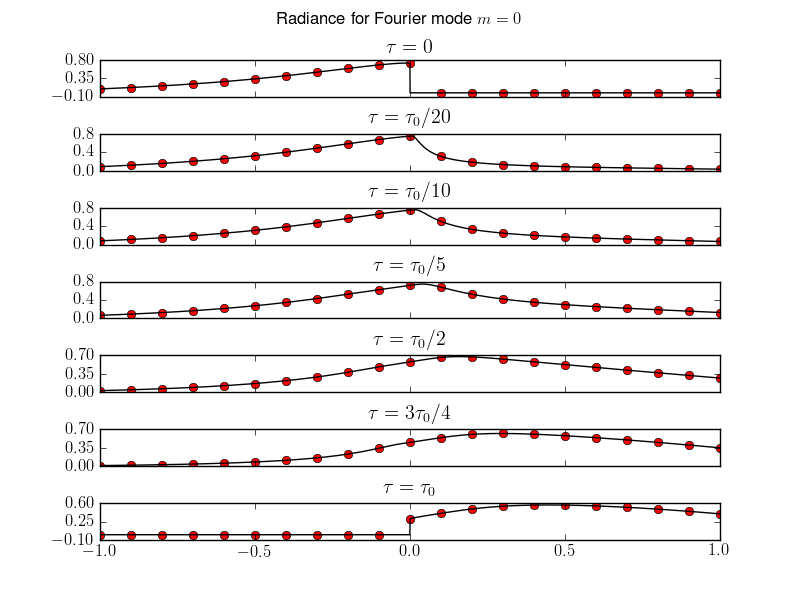
Comparison of \(m=0\) Lucee solutions (black) [s32] with GS results (red dots) for various optical depths.

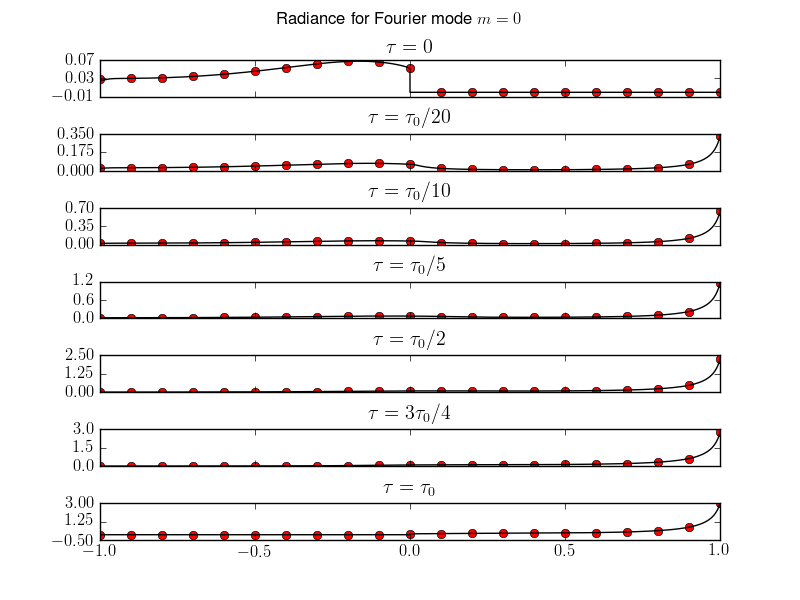
Comparison of \(m=1\) Lucee solutions (black) [s32] with GS results (red dots) for various optical depths.

Problem 2

Haze-L phase-function case with \(L=82\) for slab with \(\tau_0=1\), \(\mu_0 = 1.0\) and \(\varpi=0.9\). The expansion coefficients of the phase function are available here.

Comparison of Lucee solutions (black) [s33] with GS results (red dots) for various optical depths.

Problem 3

Same as Problem 2 except \(\mu_0=0.5\). 64 Fourier modes are used to compute the azimuthal dependence of the radiance.

Comparison of Lucee solutions (black) [s34] with GS results (red dots) for various optical depths and for \(\phi-\phi_0 = 0\).

Comparison of Lucee solutions (black) [s34] with GS results (red dots) for various optical depths and for \(\phi-\phi_0 = \pi/2\).

Problem 4

Same as Problem 2 except \(\varpi=1.0\). Note that Lucee can not actually handle this case of conservative scattering as the eigensystem is not complete when \(m=0\) and \(\varpi=1.0\). Hence, a modification of the algorithm is required to handle this by adding an eigenvector to complete the system. However, this modification is not implemented in Lucee. To overcome this we simply set \(\varpi=1-1\times 10^{-6}\).

Comparison of Lucee solutions (black) [s35] with GS results (red dots) for various optical depths.

References

Mobley1994

C.D. Mobley, Light and Water. Radiative Transfer in Natural Waters, Academic, New York, 2004.

Thomas1999

G.E. Thomas and K. Stamnes, Radiative Transfer in the Atmosphere and Ocean, Cambridge University Press, Cambridge UK, 1999.

ChandraRT

S. Chandrasekhar, Radiative Transfer, Dover Publications, 1960.

Siewert2000

C.E. Siewert, “A concise and accurate solution to Chandrasekhar’s basic problem in radiative transfer”, Journal of Quantitative Spectroscopy & Radiative Transfer, 64, Pg. 109-130, 2000. pdf.

Garcia1985

R.D.M. Garcia and C.E. Siewert, “Benchmark Results in Radiative Transfer”, Transport Theory and Statistical Physics, 14, No. 4 Pg. 437-483, 1985. pdf