JE12: Studies with a discontinuous Galerkin Poisson bracket solver
Contents
In this entry I study a discontinuous Galerkin (DG) algorithm to discretize the Poisson bracket operator. In particular, I look at the spatial and temporal convergence properties of this algorithm and study the ability of the algorithm to solve complicated problems.
The algorithm updates the equation
the Poisson bracket \(\{\chi,\psi\}\) is defined as
This equation describes the advection of the vorticity field \(\chi\) with the advection velocity determined from the potential field as \(\mathbf{u} = \nabla\psi\times \mathbf{e}_z\) or \(u_x = \partial \psi/ \partial y\) and \(u_y = -\partial \psi/ \partial x\). Hence, although \(\chi\) can be discontinuous, \(\psi\) must be be continuous.
Convergence of Poisson bracket algorithm
Temporal Convergence
In the first set of tests the temporal convergence is tested. For this a Gaussian pulse \(\chi(x,y,0) = \exp(-75(x-x_c)^2)\) is initialized, where \(x_c = 0.5\) and \(x \in [0,1]\) with periodic boundary conditions.
The potential is set to \(\psi(x,y)=y\) which advects the pulse with constant speed in the X-direction. Note that even though the problem is periodic we can not apply periodic BCs to the potential due to the linear variation in the Y direction.
Simulations were run on a \(32\times 4\) grid to \(t=1.0\). The time-steps were adjusted to CFL numbers of 0.2, 0.1, 0.05 and 0.025. To isolate the errors from the temporal discretization alone the differences in the solution were computed between successive results and their convergence computed.
The results with Runge-Kutta second-order schemes is presented in the following table.
CFL |
Change in error |
Order |
Simulation |
|---|---|---|---|
\(0.1\) |
\(4.9346\times 10^{-3}\) |
||
\(0.05\) |
\(1.2315\times 10^{-3}\) |
2.0 |
|
\(0.025\) |
\(3.0780\times 10^{-4}\) |
2.0 |
The results with Runge-Kutta third-order schemes is presented in the following table.
CFL |
Change in error |
Order |
Simulation |
|---|---|---|---|
\(0.1\) |
\(1.9146\times 10^{-4}\) |
||
\(0.05\) |
\(2.4022\times 10^{-5}\) |
2.99 |
|
\(0.025\) |
\(3.0023\times 10^{-6}\) |
3.00 |
Spatial Convergence
To test the spatial convergence of the algorithms, a Gaussian pulse is initialized and propagated diagonally across a unit square with periodic boundary conditions. The pulse returns to its starting position after unit time has elapsed. Note that diagonal propagation is a harder problem than propagation parallel to grid lines: it not only tests the isotropy of the scheme but also the ability of the scheme to capture features propagating across grid lines.
The Gaussian pulse is
where \(r = \sqrt{(x-x_c)^2+(y-y_c)^2}\) and \((x_c,y_c)\) are the coordinates of the center of the pulse. The potential is selected as
giving an advection speed of \(\sqrt{2}\) towards the top right corner of the domain. As in the previous problem, boundary conditions can not be applied to the potential. For all problems, the time-step was held fixed for all spatial resolutions.
In the first set of tests, the convergence of the second-order scheme is tested. This scheme uses the second-order 4-node Lobatto elements with RK-2 time-stepping. Grids of \(32\times 32\), \(64\times 64\) and \(128\times 128\) were used and convergence computed by comparing to the initial conditions. Results are shown in the following table.
Cell size |
Average Error |
Order |
Simulation |
|---|---|---|---|
\(1/32\) |
\(1.4036 \times 10^{-3}\) |
||
\(1/64\) |
\(2.0966\times 10^{-4}\) |
2.74 |
|
\(1/128\) |
\(4.6609\times 10^{-5}\) |
2.17 |
:doc:`s114 <../../sims/s114/s114-pb-advection-2d>`x |
The solution computed on the \(32\times 32\) grid is shown below.
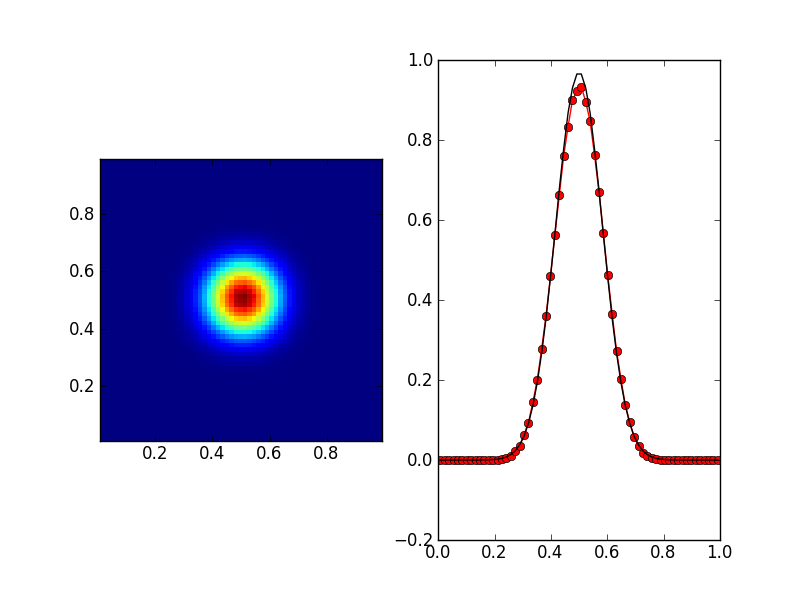
Solution computed on a \(32\times 32\) with the 2D Poisson bracket updater (left) with a slice in the X-direction (red, right) compared to exact solution (black) at \(t=0\). See s112 for input file.
In the second set of tests, the convergence of the third-order scheme is tested. This scheme uses the third-order 8-node Serendipity elements with RK-3 time-stepping. Grids of \(8\times 8\), \(16\times 16\), and \(32\times 32\) were used and convergence computed by comparing to the initial conditions. Results are shown in the following table.
Cell size |
Average Error |
Order |
Simulation |
|---|---|---|---|
\(1/8\) |
\(4.4776 \times 10^{-3}\) |
||
\(1/16\) |
\(3.4893\times 10^{-4}\) |
3.68 |
|
\(1/32\) |
\(2.8015\times 10^{-5}\) |
3.63 |
Note
To get the correct convergence with the third-order spatial scheme we need to use RK3 time-stepping. Even though the results look okay with the RK2 scheme, the mild instability in RK2 reduces the overall convergence of the spatial operator.
Rigid-body rotating flow
In this test a rigid body rotating flow is initialized by selecting the potential as
With this potential the flow velocity is \((u_x,v_x) = (-y+1/2, x-1/2)\) which represents a counter-clockwise rigid body rotation about \((x_c,y_c)=(1/2,1/2)\) with period \(2\pi\). Hence, structures in \(\chi\) will perform a circular motion about \((x_c,y_c)\), returning to their original position at \(t=2\pi\).
The simulation was performed with \(32\times 32\) and \(64\times 64\) grid with an initial cosine hump of the form
where
For this problem, \(r_0=0.2\) and \((x_0,y_0) = (1/4, 1/2)\). To test convergence, the simulation was run to \(t=2\pi\) and compared to the initial condition. Average errors of \(1.583\times 10^{-3}\) and \(3.459\times 10^{-4}\) were computed, giving a spatial convergence order of about \(2.29\). Next, a third order spatial scheme was used to compute the solution to \(t=4\pi\) at which point the cosine hump has advected twice about the origin. The figure below shows the solution at four different times, indicating that the algorithm essentially advects the initial hump without any significant distortion.
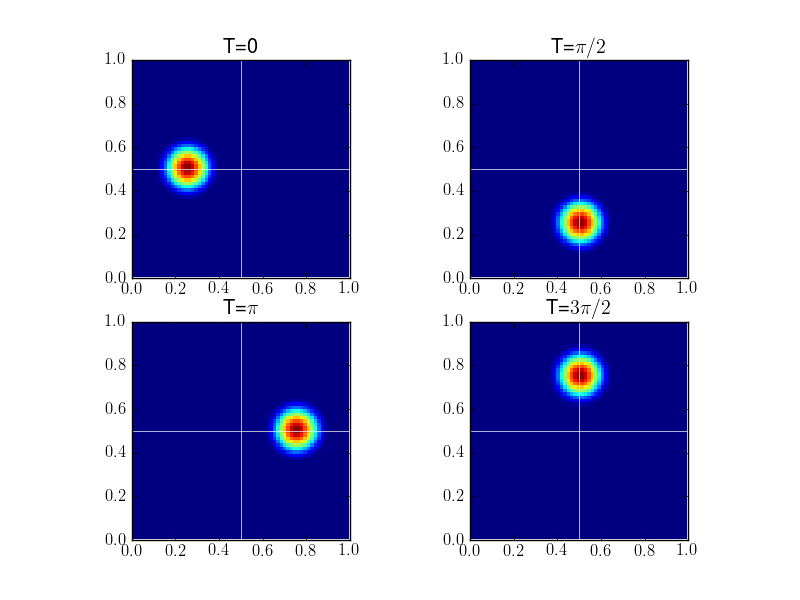
Rigid-body rotation solution on a \(32\times 32\) grid using a 3rd order discontinuous Galerkin scheme at different times [s120]. The white lines are the axes drawn through the point around which the flow rotates. These figures show that the scheme advects the initial cosine hump without significant distortion even on a relatively coarse grid. For a movie of the simulation click here.
Swirling flow
In this problem we use a time-dependent potential given by
where
With this potential we get the velocity field
This represents a swirling flow that distorts the vorticity field, reaching a maximum distortion at \(t=T/2\). At that point the flow reverses and the vorticity profile returns to its initial value.
We use a 3rd order scheme on a \(32\times 32\) grid and run the simulation to \(t=2T\). The results are show in the following figure. For a movie of the simulation click here.

Swirling flow solution on a \(32\times 32\) using a 3rd order discontinuous Galerkin scheme at different times [s121]. The figure shows the initial condition, the maximum distortion in the first half period after which the solution returns to its initial value, swinging back for a second oscillation.
In the following figure compares the final solution to the initial conditions.
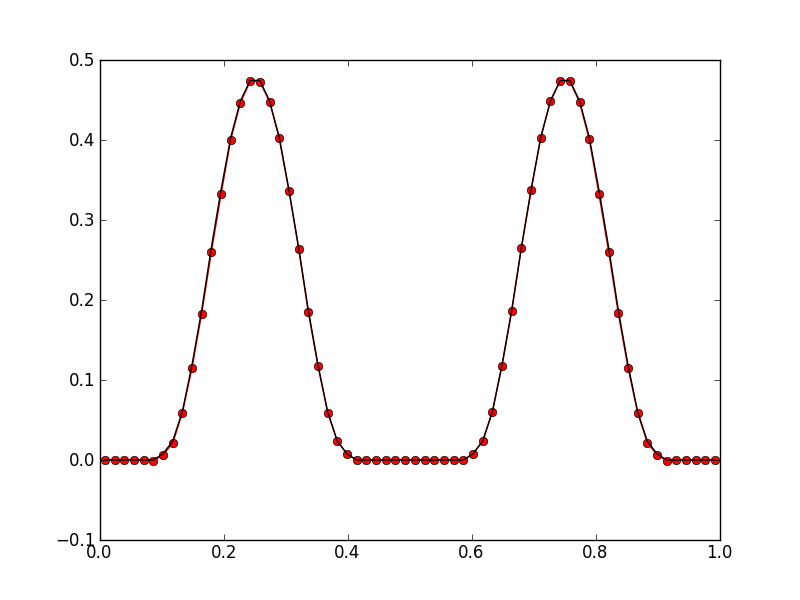
Swirling flow solution on a \(32\times 32\) grid using a 3rd order discontinuous Galerkin scheme at \(t=2T\) (red dots) compared to the initial conditions (black line). The algorithm is able to handle this complicated flow pattern and show very little distortion of the final solution. See [s121].
Enstrophy conservation properties
For equation (1) there are an infinite set of invariants. Let \(C_a(\chi)\) be an arbitrary function. Then the scalar quantity
is conserved. In particular, \(C_a = \chi^2/2\) is called the fluid enstrophy. To prove conservation, multiply (1) by \(C_a'(\chi)\) after writing \(\{\chi,\psi \} = \mathbf{u}\cdot \nabla \chi\) and integrate over the domain, using the boundary conditions to get
We can show that the Poisson bracket algorithm does not conserve enstrophy unless a central flux is used. Even with the central flux the overall scheme is not conservative as the Runge-Kutta time-stepping adds a small amount of diffusion.
The following figure shows the error in enstropy as the time-step is reduced. The error should reduce with the same order as the time-stepping order, in this case third. These simulations were run with central flux with the DG2 spatial scheme.
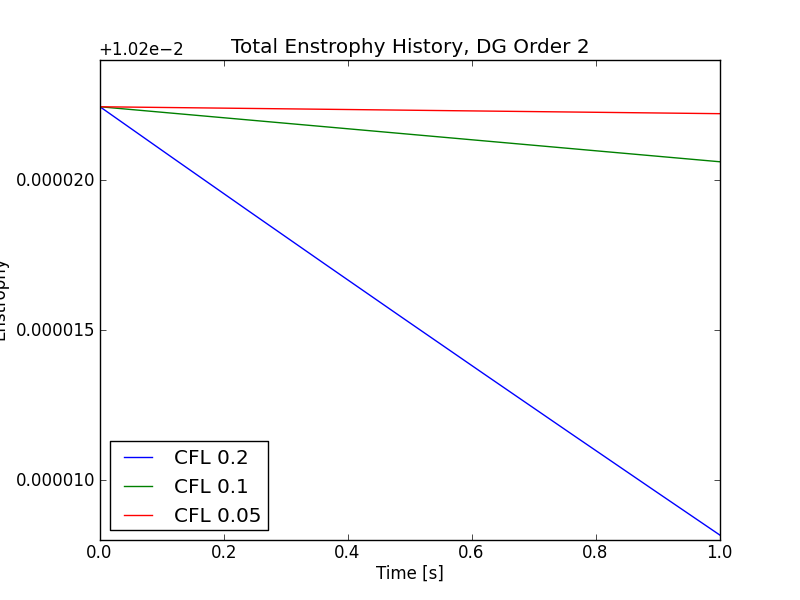
Enstrophy history with different CFL numbers. The relative errors in enstrophy in are \(1.396\times 10^{-3}\), \(1.794\times 10^{-4}\) and \(2.254\times 10^{-5}\), giving a convergence order 2.96 and 2.99 respectively. See s122, s123 and s124, for input files.