JE20: Vlasov equation on bounded domain

In many practical problems of interest the Vlasov equation needs to be solved on a domain bounded by walls. In this document I describe the boundary conditions for such bounded domain simulations and present some example calculations the case of free-streaming particles, with specified electric potential and for a simple plasma sheath. For periodic domain calculations, see JE14 and JE15.

Free-streaming

Consider the Vlasov equation with zero potential (free streaming of particles)

\[\frac{\partial f}{\partial t} + v\frac{\partial f}{\partial x} = 0\]

on \(x\in[0,L]\), where \(f(x,v,t)\) is the distribution function. Let \(f(x,v,0)=f_0(v)\) be the initial condition, and assume that the particles streaming into the wall are completely absorbed. The boundary condition can be hence written as

\[\begin{split}f(0,v,t) &= 0 \\ f(L,-v,t) &= 0\end{split}\]

for \(v>0\). In Gkeyll these boundary conditions are implemented by simply setting the distribution function to zero in the ghost cells. Proper upwinding insures that all the particles flow out of the domain and none enter.

The total number of particles in the domain, \(n(t)\), can be computed analytically as follows. There are \(f_0(v)dv\) particles with velocity \(v\) and spread \(dv\). Hence, after time \(t\) the number of particles with that velocity will be \((L-vt)f_0(v)dv\). Also, after time \(t>L/v\) all particles with velocity \(v\) will have been absorbed by the wall. Hence, we can write

\[n(t) = \int_0^{L/t} (L-vt) f_0(v) dv + \int_0^{L/t} (L-vt) f_0(-v) dv.\]

Here the first integral accounts for the particles flowing out of the right wall, and the second the particles flowing out of the left wall.

To test the boundary conditions a simulation was run on \(x\in[0,2\pi]\) with \(f_0(v)\) initialized to a Maxwellian

\[f_0(v) = \frac{n_0}{\sqrt{2\pi v_t^2}} e^{-v^2/2v_t^2}\]

with \(n_0=v_t=1\). A grid of \(16\times 32\) was used with piece-wise quadratic Serendipity basis functions. The number of particles in the domain was compared to the exact solution. The results are shown below.

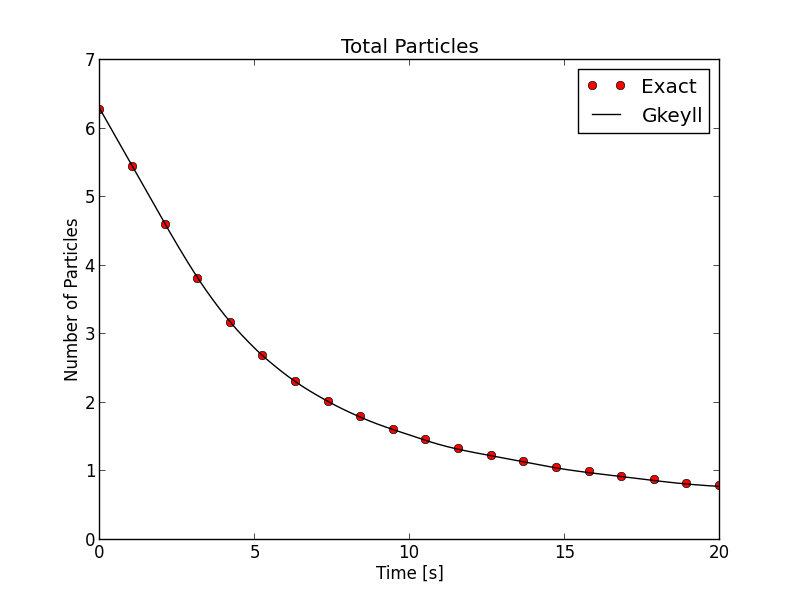
Total number of particles in domain computed by Gkeyll (black line) compared to the exact solution (red dots) as a function of time. The walls in this simulation are assumed to be perfectly absorbing. See [s254] for details.