JE24: Tests for stair-stepped boundary Euler solver
Contents
Warning
There is a subtle bug in the present implementation, which I have not been able to track down. Basically, when running in parallel, if the MPI domain boundary and the embedded boundaries are coincident or separated by one cell, the results differ very slightly from serial results. Note that for all other cases in parallel the bug does not manifest itself.
In this note I test the finite-volume embedded boundary updater on the Euler equations. At present, Gkeyll uses a stair-stepped mesh to represent the surface of an object. Although crude, this is sufficient to tackle many problems, including magnetosphere modeling. We are interested in the latter problem, and most global magnetosphere codes use a stair-stepped mesh to represent the planet/moon surface. The representation of the boundary may be improved in the future by using either a conformal cut-cell mesh, or using a multi-block body-fitted mesh. Note that for viscous flows, using stair-stepped or even cut-cell BCs is not a good idea as near a wall, to capture the boundary layer accurately, one needs meshes aligned with the surface.
For now, stair-stepped meshes are sufficient.
Note on geometry representation and embedded boundary conditions
The key step in doing embedded boundary simulations is to setup the geometry. For this, one needs to create an Gkeyll field with a single component. This field should store a positive number when the corresponding point is inside the domain and a negative number when it is outside the domain. Rather complex objects can be created by combining a set of elementary shapes (circles, boxes, ellipses, …) using shift/rotate and logical operators. For example, to represent a circle one can use the Lua function
function inCircle(x,y, xc,yc,rad)
return (x-xc)^2 + (y-yc)^2 < rad^2 and 1.0 or -1.0
end
This function evaluates to 1.0 when inside the sphere, and to -1.0 otherwise. Note that for flow around a sphere one needs to flip the signs in the above equation.
Given two in/out functions \(d_A(x,y)\) and \(d_B(x,y)\) can can create a new functions representing the union, intersection and subtraction as follows
In three dimensions several other operations are possible: rotation of a 2D shape about some axis, extrusion of a 2D shape along a curve, etc. Arbitrary shapes can be represented in this way, however, the final function representing a complex shape may not be very readable.
Once the object geometry has been created, the boundary condition update needs to be created (in 2D) using the StairSteppedBc2D updater. This updater takes in the in/out field and a list of BCs to apply.
Note that due to the way in which BCs are applied this updater also needs the direction in which to apply the BC (using a setDir method). In essence, I am assuming that this updater is used as part of a dimensionally-split algorithm in which the BC is applied in a particular direction and then the update in that direction is performed. For unsplit algorithms, embedded BCs require more complicated data-structures.
Note on numerical fluxes
In most of these simulations, I need to use HLLE fluxes (enabled using numericalFlux = “lax” and useIntermediateWave = true in HyperEquation.Euler constructor). The Roe fluxes causes severe problems, including carbuncle problem and launch of spurious shocks from stair-stepped cells.
It appears that the numerical diffusion added by the HLLE flux effectively acts to “smooth out” the jagged representation of the boundary (effectively creating a numerical boundary layer), allowing one to obtain reasonable results. However, as is obvious (and shown below) if the flow is very sensitive to the flow along the boundary, then stair-stepped meshes are not a good idea, and one will need to use a body-fitted (structured or unstructured) mesh.
One should also keep in mind that using HLLE (or any diffusive flux) with the WavePropagationUpdater is not usually a good idea: the solution quality is very sensitive to the numerical flux, and best results are usually obtained when using Roe fluxes.
Double Mach reflection
In this problem, a Mach 10 shock reflects off a 30 degree ramp, forming a complex Mach stem that separates the fluid into several regions with different flow properties. This problem has been extensively studied in the literature.
The shock is created using an initial state, with \(\rho=8, u = 8.25, p=116.5\) for \(x<0.5\) and \(\rho=1.4, u = 0, p=1.0\) for \(x>0.5\). The domain is \(3\times 2\) and a grid of \(450\times 300\) is used. The wedge tip is at \(x=0\). The density at \(t=0.2\) is shown below.
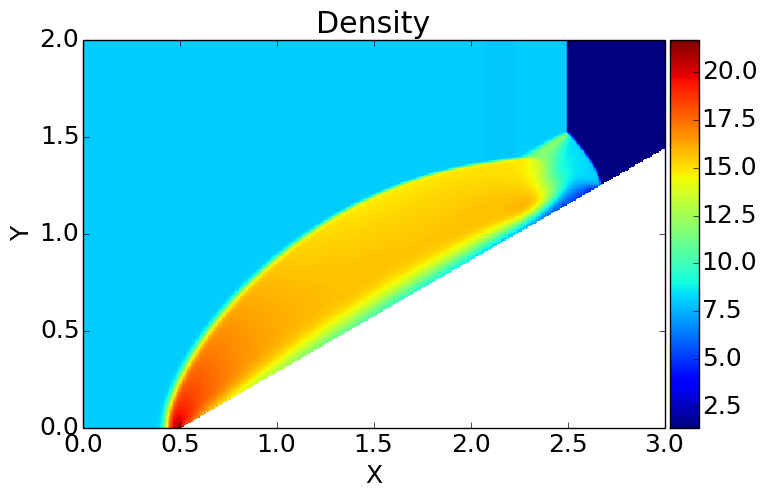
Density for double Mach reflection problem at \(t=0.2\). A Mach 10 shock interacts with a 30 degree wedge, forming a curved shock and a complex triple Mach stem. This simulation uses a HLLE flux. Compared to published results, the Gkeyll results with stair-stepped boundaries look correct. However, notice the formation of a spurious boundary layer due to the numerical diffusion from the HLLE flux. See [s418] for input file.
Notice that the solution using the HLLE flux is rather diffusive and shows the formation of a spurious boundary layer. The simulation was repeated using Roe flux, which is less diffusive, and compared with the results obtained from the HLLE flux. The results are shown below.

Density (left column) and pressure (right column) for double Mach reflection problem at \(t=0.2\). The upper row results were obtained using a Roe flux [s419] and the lower row, with HLLE flux [s418]. The Roe flux results are sharper, resolving the Mach stem better, and do not have the spurious boundary layer on the wedge surface. However, the use of a stair-stepped boundary launches a series of spurious oblique shocks in the Roe flux simulation.
Although the Roe flux solution is sharper, resolving the Mach stem better, spurious oblique shocks are launched from the stair-stepped wedge surface. In contrast, the HLLE solution does not show these spurious shocks, however, the results are more diffuse and a numerical boundary layer is formed.
Shock interaction with cylinder
In this problem I study the interaction of a Mach 2 shock with a cylinder of radius \(0.15\). The shock starts at \(x=-0.3\), with pre-shock values of \(\rho=1.4, p=1.0\). The shock interacts with the cylinder, creating a Mach stem, separating the flow into three regions. The problem has been studied by Berger et. al. 1 using a cut-cell approach.
The density and pressure at \(t=0.25\) from a \(300\times 300\) simulation are shown below.
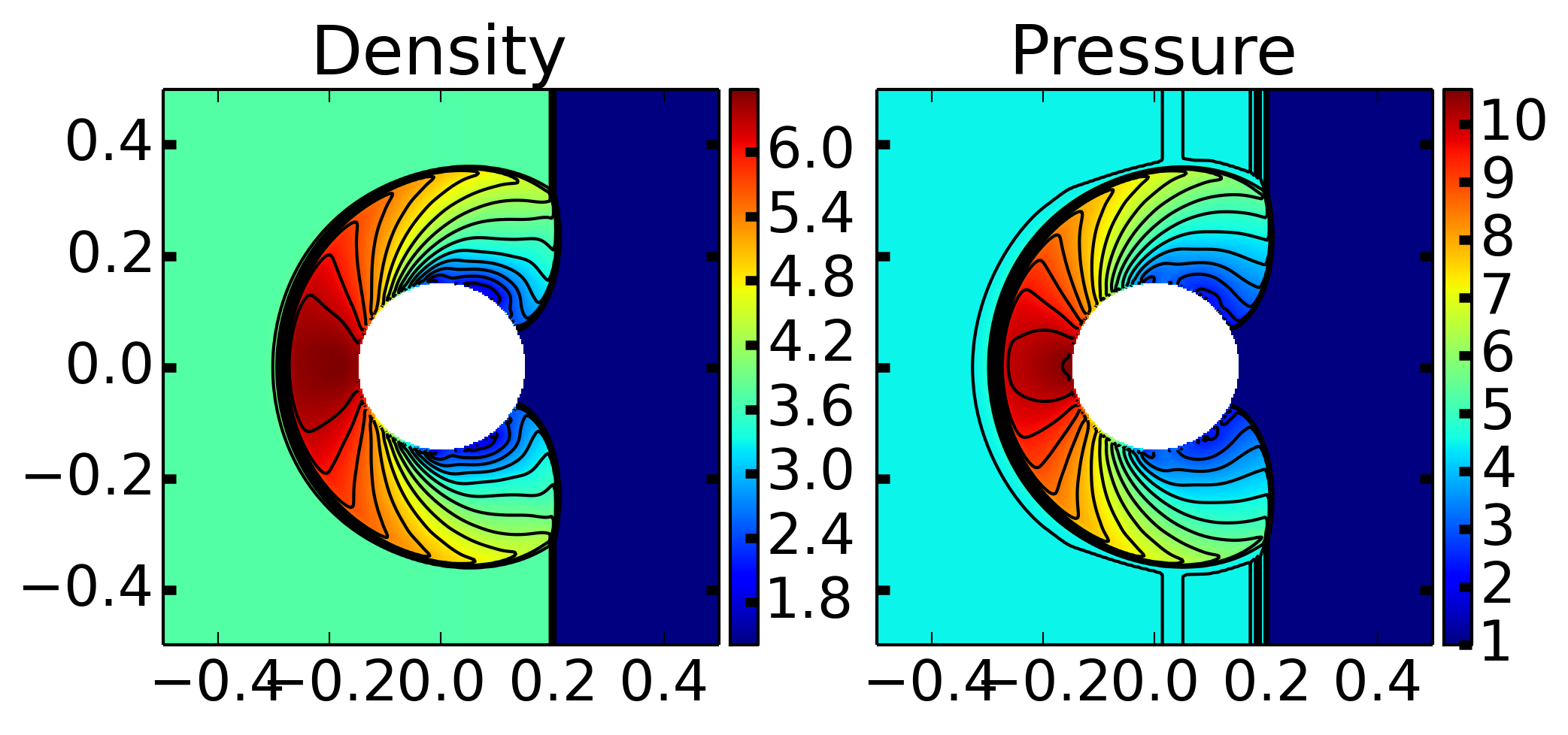
Density (left) and pressure (right) from a Mach 2 shock interaction with a circular cylinder at \(t=0.25\) on a \(300\times 300\) grid. See [s420] for details. A triple Mach stem is formed, dividing the fluid into three distinct regions. The results are visually very similar to the ones presented by Berger et. al. 1, who solved the problem using a cut-cell approach.
The results shown above compare very well with those presented by Berger et. al. 1. Note that this case is in contrast to the previous two problems, in which the solution quality was relatively poor. The reason for this is that once the shock stands-off from the cylindrical surface, the stair-stepped boundary influences the rest of the flow only weakly.
To test the algorithm on a more complex geometry, the interaction of a Mach 3 shock with two cylinders is studied. The pressure at \(t=0.096\) and \(t=0.16\) are shown below. The results are in excellent agreement with those presented in 1.
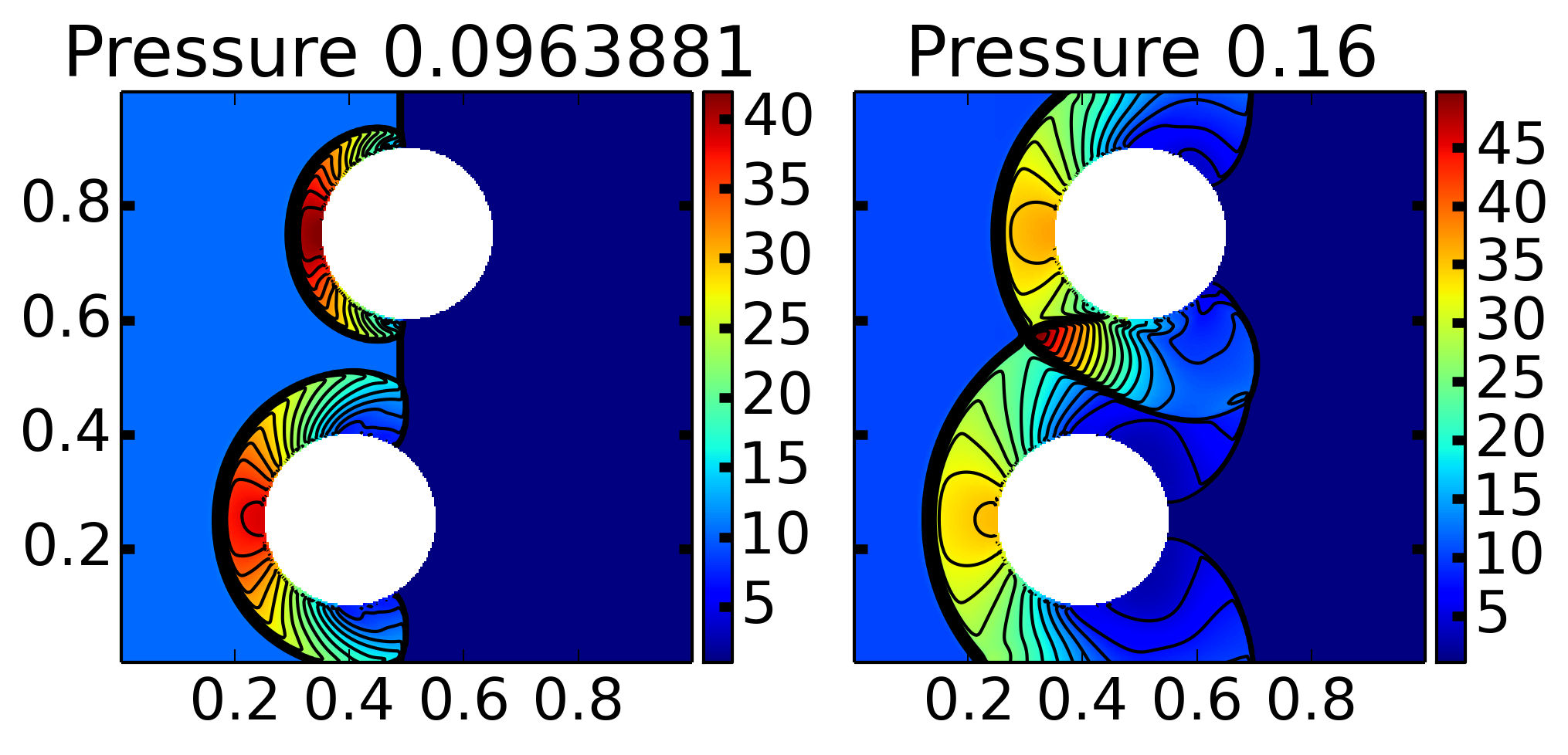
Density from a Mach 3 shock interaction with two circular cylinders centered at \((0.4,0.35)\) and \((0.5,0.75)\) on a \(300\times 300\) grid. See [s422] for details.The results are in excellent agreement with those presented by Berger et. al. 1, who solved the problem using a cut-cell approach.
Supersonic flow over blunt body
In this problem I study supersonic flow over a ellipsiod with circular cross-section. This allows one to treat the problem using a 2D axi/symmetric solver. For note on the axisymmetric solver see JE23. The ellipsoid is given by
with \(a=b=1/4\) and \(c=1/2\). The free-stream flow is Mach 2 directed in the negative \(Z\) direction, with \(\rho=1\) and \(p=1\). The domain is \((r,z)\in [0,1]\times[0,2]\) and grid \(100\times 200\).
Density and pressure near steady-state are shown below. A detached bow shock forms on the object. The flow in the downstream side seems not to be in steady-state, however.
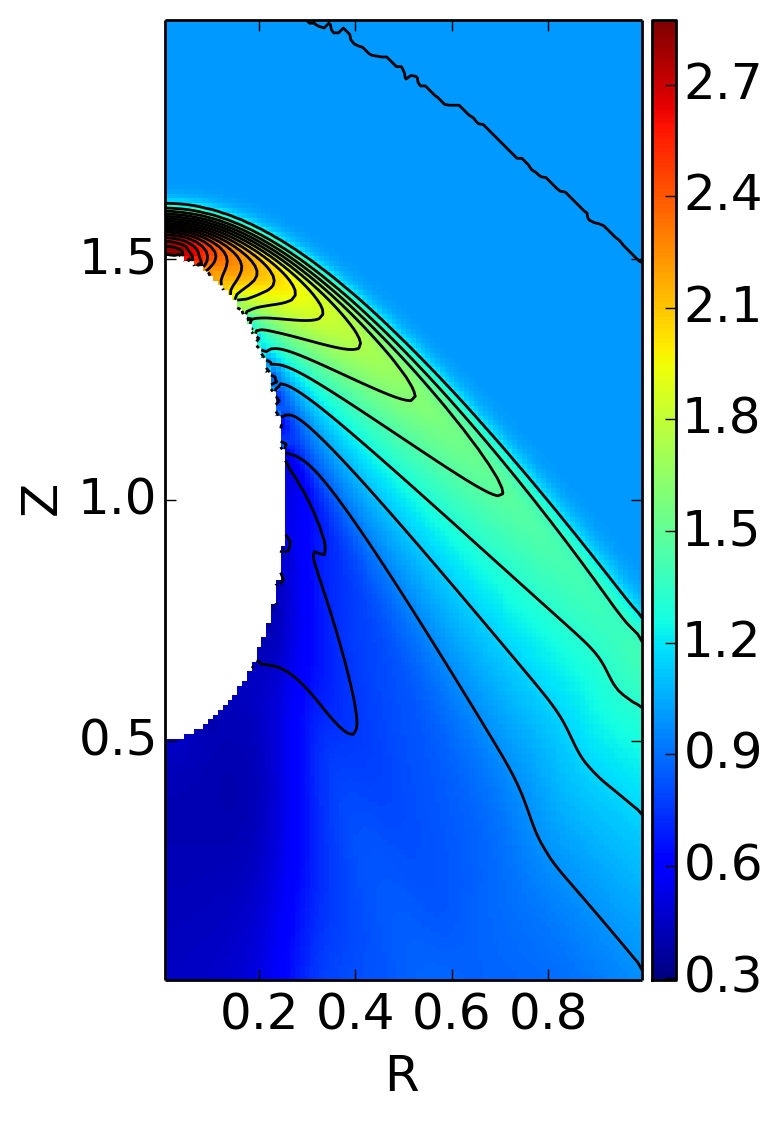
Density and superimposed pressure contours for Mach 2 flow over an ellipsoid with circular cross section. An axisymmetric solver was used to solve the Euler equations. See [s423] for details. A detached bow shock forms over the nose of the ellipsoid.
The same problem was setup using a full 3D solver. This allows testing of the 3D solver by comparing to axisymmetric results.
Two different resolutions were used: \(50\times 50\times 100\) and \(100\times 100\times 200\). Symmetry boundary conditions were used at \(X=0\) and \(Y=0\). Flow conditions were identical to the axisymmetric problem described above.
The following figure shows the density and pressure contours from the \(100\times 100\times 200\) simulation. These compare very well with the axisymmetric result shown above, giving some confidence that the 3D code is working correctly.
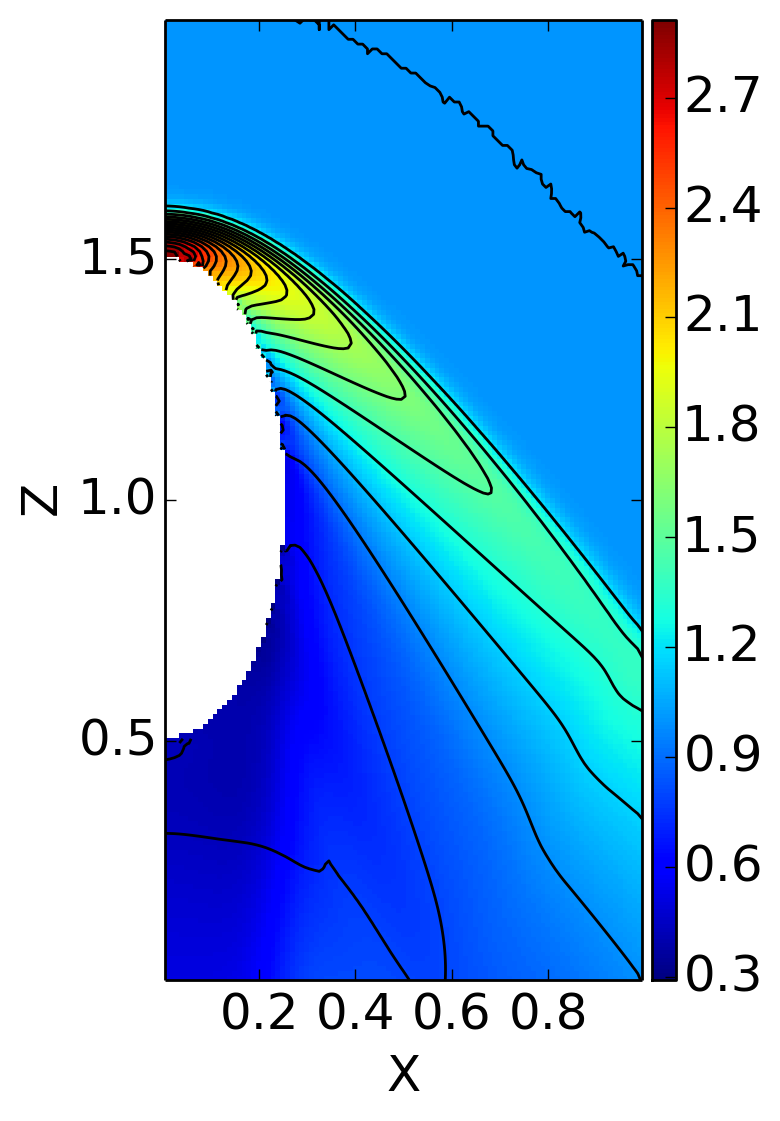
Density and superimposed pressure contours in the \(X-Z\) plane for Mach 2 flow over an ellipsoid with circular cross section. An 3D solver was used to solve the Euler equations. See [s425] for details. The 3D results compare very well with the 2D axisymmetric results shown above, giving some confidence that the 3D code is working correctly.
A more quantitative comparison between the 3D and 2D axisymmetric results can be obtained by computing radial lineouts from the 3D results and comparing it with the 2D results. This is shown in the figure below.
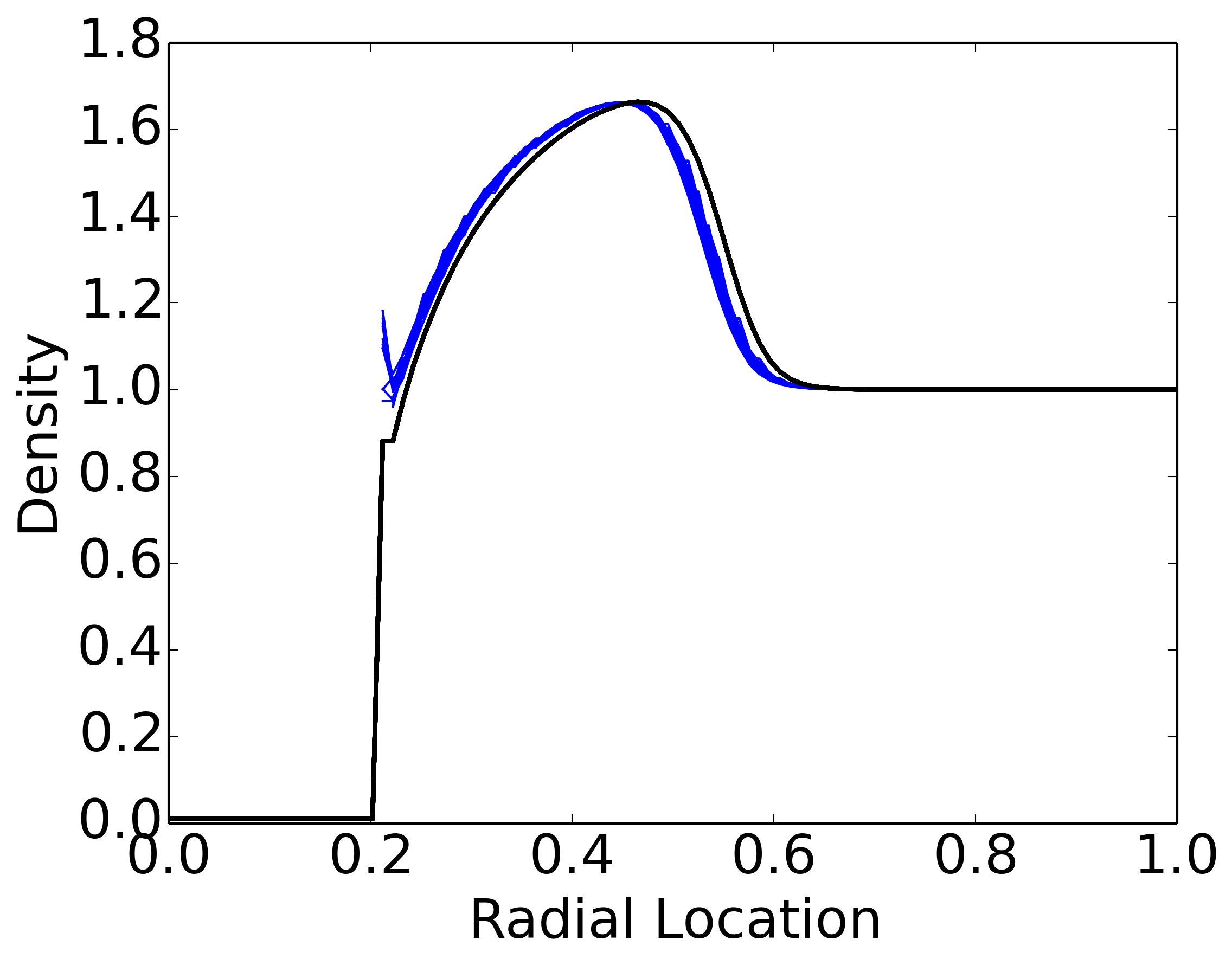
Scatter plot of density (blue lines) from 3D simulation, compared to 2D axisymmetric results (black line), computed at \(Z=1.25\). The 3D and 2D axisymmetric results compare reasonably well, except for a small shift. (These could just be a plotting issue or a small difference in which in/out fields are evaluated in 2D v/s 3D).
Conclusions
I have performed basic tests of the stair-stepped boundaries in Gkeyll. The key conclusion is that although stair-stepped boundaries are easy to setup, the results are not very satisfactory for some problems. For shock problems, in which shock angles, jump conditions sensitively depend on geometry, a better boundary representation should be used. However, the solutions give a qualitative indication of the flow features.
For some problems, in particular shock interaction with embedded objects, in which the shock standoff distance is significant, the use of stair-stepped boundaries gives high-quality results comparable to cut-cell conformal boundary methods.
For magnetosphere problems the shock properties depend on magnetic field structure rather than the geometry of the planet/moon surface. Hence, the impact of the stair-stepped boundary will be likely weak. However, this remains to be verified.