JE5: Hyperbolic balance laws with dispersive source terms

Contents

• JE5: Hyperbolic balance laws with dispersive source terms

  • Linearization and hyperbolic balance laws with dispersive sources

  • The Dispersive Euler Equations

  • Exact solution for initial step function perturbation

  • A note on solving dispersive Euler equations with Lucee

  • Problem 1: Case \(\omega_c = 10\)

  • Problem 2: Case \(\omega_c = 100\)

  • Problem 3: Sod-shock problem

  • Conclusions

While solving the two-fluid Riemann problems small oscillations are observed in the solution. On first sight it might be thought that these oscillations are numerical and do not reflect a correct solution to the ideal two-fluid equation system. In this note I show that such solutions can (and do) occur when certain types of source terms are present and the homogeneous system is hyperbolic.

Linearization and hyperbolic balance laws with dispersive sources

Linearizing a hyperbolic balance law can lead to important insights into the structure of solutions, although linearization can not reveal the rich non-linear phenomena (shocks, rarefactions and contact discontinuities) that are described by these equations. We start from the non-conservative form of the equations

\[\frac{\partial \mathbf{v}}{\partial t} + \mathbf{A}_p\frac{\partial \mathbf{v}}{\partial x} = \mathbf{s}_p\]

where \(\mathbf{v}\) are the primitive variables, \(\mathbf{A}_p\) is a Jacobian matrix and \(\mathbf{s}_p\) are source terms. Linearize about a uniform equilibrium \(\mathbf{v}_0\) to write \(\mathbf{v} = \mathbf{v}_0 + \mathbf{v}_1\), where \(\mathbf{v}_1\) is a small perturbation. Using a Taylor series expansion to first-order to write \(\mathbf{s}_p(\mathbf{v}) = \mathbf{s}_p(\mathbf{v}_0) + \left( {\partial \mathbf{s}_p}/{\partial \mathbf{v}} \right)_{\mathbf{v}_0} \mathbf{v}_1\) and \(\mathbf{A}_p(\mathbf{v}) = \mathbf{A}_p(\mathbf{v}_0) + \left( {\partial \mathbf{A}_p}/{\partial \mathbf{v}} \right)_{\mathbf{v}_0} \mathbf{v}_1\) and letting \(\mathbf{M}_p \equiv {\partial \mathbf{s}_p}/{\partial \mathbf{v}}\), the linear form of the non-conservative equation becomes

\[\frac{\partial \mathbf{v}_1}{\partial t} + \mathbf{A}_p(\mathbf{v}_0)\frac{\partial \mathbf{v}_1}{\partial x} = \mathbf{M}_p(\mathbf{v}_0)\mathbf{v}_1.\]

To understand the mathematical structure of the linear equation a Fourier representation of the solution is assumed and each mode is represented as \(\mathbf{v}_1 = \mathbf{\hat{v}}_1 e^{i\omega t} e^{i k x}\), where \(\omega\) is the frequency and \(k\) is the wavenumber. Using this we obtain

\[\left[ i\omega\mathbf{I} + ik\mathbf{A}_p(\mathbf{v}_0) - \mathbf{M}_p(\mathbf{v}_0) \right] \mathbf{v}_1 = 0,\]

where \(\mathbf{I}\) is a unit matrix. For non-trivial solutions the determinant of the matrix in the square brackets must vanish. Another way to state this condition is that the frequency and wavenumbers must be related by the dispersion relations \(\omega = \omega(k)\) which are the eigenvalues of the matrix \(-k\mathbf{A}_p(\mathbf{v}_0) - i\mathbf{M}_p(\mathbf{v}_0)\). Thus if \(\lambda^p(k,\mathbf{v}_0)\) is the \(p^{\textrm{th}}\) eigenvalue of this matrix then the \(p^{\textrm{th}}\) branch of the dispersion relation is \(\omega = \lambda^p(k,\mathbf{v}_0)\).

If the dispersion relation is purely real then the equation system will support non-decaying waves. Further, if the dispersion relation is linear, then a wave packet will propagate without distortion. If, however, if the dispersion relation is non-linear (but still real), the wave packet will suffer dispersion, i.e. waves with different wave-numbers will propagate with different group and phase speeds.

For the simple case of vanishing sources (\(\mathbf{s}_p=0\)) the dispersion relation reduces to \(\omega = \lambda^p k\), where \(\lambda^p\) are the eigenvalues of the Jacobian matrix \(\mathbf{A}_p\). As the homogeneous equation is assumed to be hyperbolic the eigenvalues are all real, indicating that for the homogeneous case waves will propagate without dispersion or decay.

This simple analysis indicates that the linear solution will depend on the nature of the eigenvalues of the source Jacobian matrix \(\mathbf{M}_p\). In case the eigenvalues of this matrix are purely imaginary, the dispersion relation will be real but waves will suffer dispersion as they propagate in the background uniform equilibrium. In this case the system of equations is called hyperbolic balance laws with dispersive source terms. (This is my own terminology and I have not seen such equations discussed in the literature).

The Dispersive Euler Equations

Several simple hyperbolic balance laws with dispersive source terms can be constructed. However, a particularly useful system that has properties similar to the ideal two-fluid equations is the following dispersive Euler system

\[\begin{split}&\frac{\partial \rho}{\partial t} + \nabla\cdot(\rho\mathbf{u}) = 0 \\ &\frac{\partial \mathbf{u}}{\partial t} + \mathbf{u}\cdot\nabla\mathbf{u} = -\nabla p/\rho + \lambda\mathbf{u}\times\mathbf{b} \\ &\frac{\partial p}{\partial t} + \mathbf{u}\cdot\nabla p = -\gamma p \nabla\cdot\mathbf{u}\end{split}\]

where \(\mathbf{b}(\mathbf{x})\) is a time-independent vector field and \(\lambda\) is a constant.

Consider solving the linearized system in one-dimension. Linearizing around stationary uniform initial state \(\rho = \rho_0\), \(p = p_0\) and assuming \(\mathbf{b} = (0,0,b_z)\), where \(b_z\) is constant leads to the linear system

\[\begin{split}\frac{\partial \rho_1}{\partial t} &= -\rho_0\frac{\partial u_1}{\partial x} \\ \rho_0\frac{\partial u_1}{\partial t} &= -\frac{\partial p_1}{\partial x} + \rho_0 \lambda v_1 b_z \\ \rho_0\frac{\partial v_1}{\partial t} &= -\rho_0 \lambda u_1 b_z \\ \frac{\partial p_1}{\partial t} &= -\gamma p_0 \frac{\partial u_1}{\partial x}\end{split}\]

Assuming solutions of the form

\[f(x,t) = \sum_{n=0}^\infty f_n e^{i(k_n x + w_n t)}\]

for \(f\in \{\rho_1,u_1,v_1,p_1\}\) and \(k_n\) is the wave number and \(\omega_n\) is frequency we get the algebraic equations

\[\begin{split}i \omega_n \rho_1 &= - i k_n u_1 \rho_0 \\ i \omega_n u_1 \rho_0 &= -i k_n p_1 + \lambda v_1 b_z \\ i \omega_n v_1 \rho_0 &= - \rho_0 \lambda u_1 b_z \\ i \omega_n p_1 &= i \gamma p_0 k_n u_1.\end{split}\]

From this the dispersion relation can be computed as

\[\omega_n = \pm ( k_n^2 c_{s0}^2 + \omega_c^2 )^{1/2}\]

Here \(c_{s0} \equiv \sqrt{\gamma p_0/\rho_o}\) is the speed of sound and \(\omega_c \equiv \lambda b_z\) is the eigenvalue of the source Jacobian.

Exact solution for initial step function perturbation

Consider a initial perturbation of the form \(u(x,0)\) where

\[u_1(x,t) = U_0 \sum_{n=0}^N \frac{i}{2n+1} e^{i k_nx} e^{i \omega_n t}\]

with \(k_n = 2\pi(2n+1)\). For \(N\rightarrow \infty\) this represents the propagation of a step function perturbation. Letting \(u_i^{(n)} \equiv i U_0 /(2n+1) e^{i(k_nx+\omega_nt)}\) the Fourier components of the other flow variable perturbations are given by

\[\begin{split}\rho_1^{(n)} &= -\frac{k_n\rho_0}{\omega_n} u_1^{(n)} \\ v_1^{(n)} &= -i\frac{\lambda b_z}{\omega_n} u_1^{(n)} \\ p_1^{(n)} &= -\frac{\gamma k_n p_0}{\omega_n} u_1^{(n)},\end{split}\]

summing which over \(n=0,\ldots,N\) gives the exact solution to the linear problem. The following figure shows the exact solution for \(N=5000\), \(\omega_c = 10\) and \(c_s = \sqrt{2}\) at time 1000.

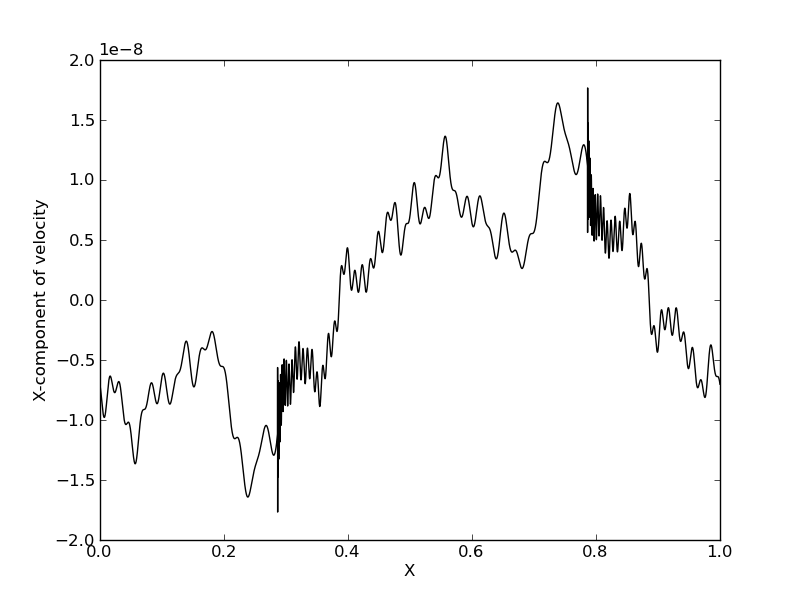
Exact solution [s41] of the linear dispersive Euler equation for \(N=5000\), \(\omega_c = 10\) and \(c_s = \sqrt{2}\) at time 1000. Very fine small-scale features are seen which, in a numerical solution, might be mistaken for numerical noise.

A note on solving dispersive Euler equations with Lucee

The dispersive Euler equations can be solved by adding a source term to the Euler equations. The source terms can be implemented using a Lorentz force object. This object needs an electric and magnetic field as input. Hence, we need to allocate memory for all the field components and set the electric field to zero. Due to the peculiarity of the point ODE integrator, this memory needs to be part of the fluid fields. Hence, in the simulations shown below (see, for example, s40) the fields have 11 components (5 for fluids and 3 for electric field and 3 for magnetic field).

Problem 1: Case \(\omega_c = 10\)

A series of simulations was performed for the case of \(\omega_c = 10\) and \(c_s = \sqrt{2}\). To avoid exciting all the Fourier modes in the step function, the expansion was carried out to only \(N=9\) modes. The solution was computed on grids of 100, 200, 300 and 400 cells. The results of velocity \(u(x,t)\) are shown below at \(t=3\). The wave-propagation scheme has intrinsic diffusion due to which the small wavelength features are poorly resolved when the grid is relatively coarse.

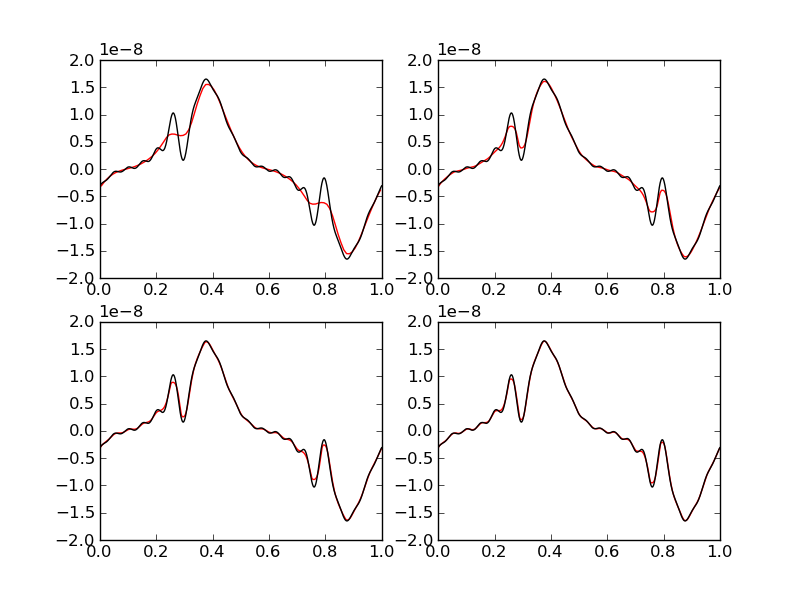
Velocity at \(t=3\) for \(\omega_c = 10\) for different grid resolutions. The red lines are the numerical results while the black lines is the exact solution. The top-left figure shows 100 cell results [s40], top-right 200 cell results [s42], bottom-left 300 cell results [s43] and bottom-right 400 cell results [s44]. At low resolution the small wavelength features are poorly resolved due to numerical diffusion of the scheme.

Problem 2: Case \(\omega_c = 100\)

In these simulations, the influence from sources was increased by setting \(\omega_c = 100\). The simulation is run on a grid with 200 cells. The time-step for this case is constrained by the need to resolve the oscillations from the source terms. Taking \(k \approx 1/\Delta x = 1/200\) we get the largest frequency as approximately 283. To resolve this the time-step needs to much smaller than \(1/238 \approx 0.0035\). This forces a more restrictive CFL number (0.5) than allowed by stability of just the hyperbolic part. If the oscillations are not resolved significant phase errors are seen in the solution.

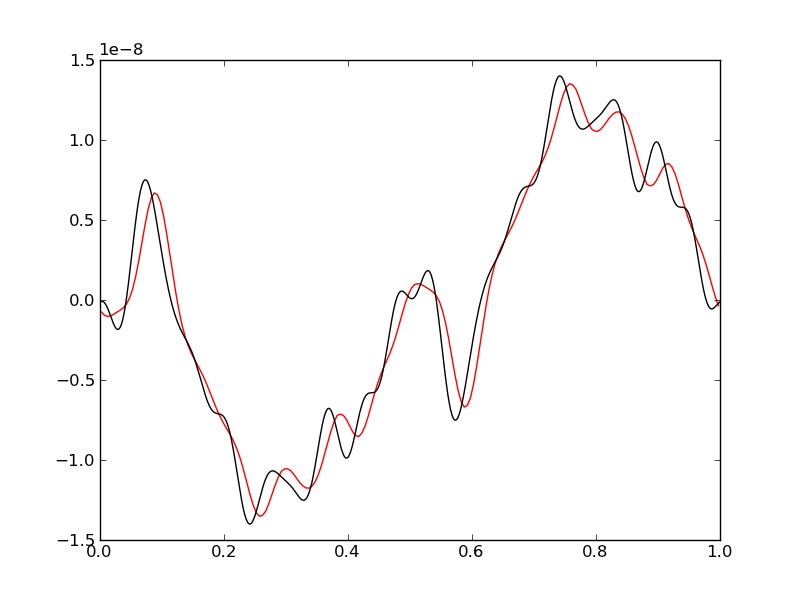
Velocity at \(t=3\) for \(\omega_c = 100\) with 200 cells [s48] and with a CFL number of 0.9. The red line is the numerical result while the black line is the exact solution. The numerical solution is not only highly diffuse but the peaks are not in the correct location, showing phase errors in resolving the oscillations from the dispersive terms. The reason for these phase errors, even though the time-step satisfies the fluid CFL condition, is that the oscillation period of the smallest wavenumber waves is not adequately resolved.

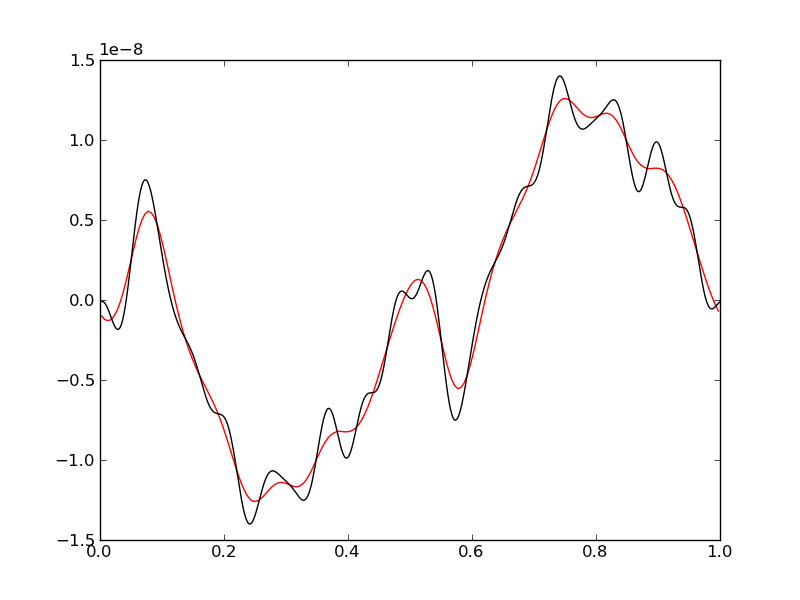
Velocity at \(t=3\) for \(\omega_c = 100\) with 200 cells [s45] with a CFL number of 0.5. The red line is the numerical result while the black line is the exact solution. Significant diffusion is seen in the results as well as small phase errors. Taking an even smaller time step will reduce the phase error but add even more diffusion.

The simulation was next run with 400 cells. This significantly improves the numerical solution even though some small-scale features are still not resolved correctly.

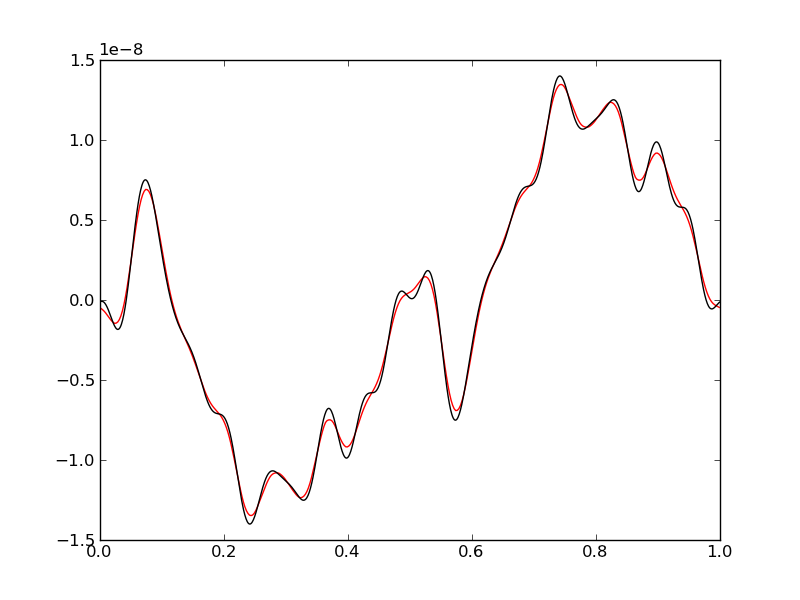
Velocity at \(t=3\) for \(\omega_c = 100\) with 400 cells [s46]. The red line is the numerical result while the black line is the exact solution. The solution is now much better resolved, although some small scale features are not resolved well.

Problem 3: Sod-shock problem

The previous simulations show the effect of dispersive source terms on linear problems. In this simulation I solve the sod-shock problem for the dispersive Euler equations. This is a highly non-linear problem and shows complex shock structure. The problem is initialized with a discontinuity at \(x=0.5\) and with left and right states

\[\begin{split}\left[ \begin{matrix} \rho_l \\ p_l \end{matrix} \right] = \left[ \begin{matrix} 3.0 \\ 3.0 \end{matrix} \right], \qquad \left[ \begin{matrix} \rho_r \\ p_r \end{matrix} \right] = \left[ \begin{matrix} 1.0 \\ 1.0 \end{matrix} \right].\end{split}\]

and is run to \(t=0.1\) on a grid of 800 cells with \(\mathbf{b} = (0.75, 0.0, 1.0)\), \(\lambda=100\) and \(\gamma = 5/3\).

The results are shown below. These show significant differences between the zero-source case and the one with the dispersive sources. Note that the solution looks like the two-fluid solutions to the Riemann problem.

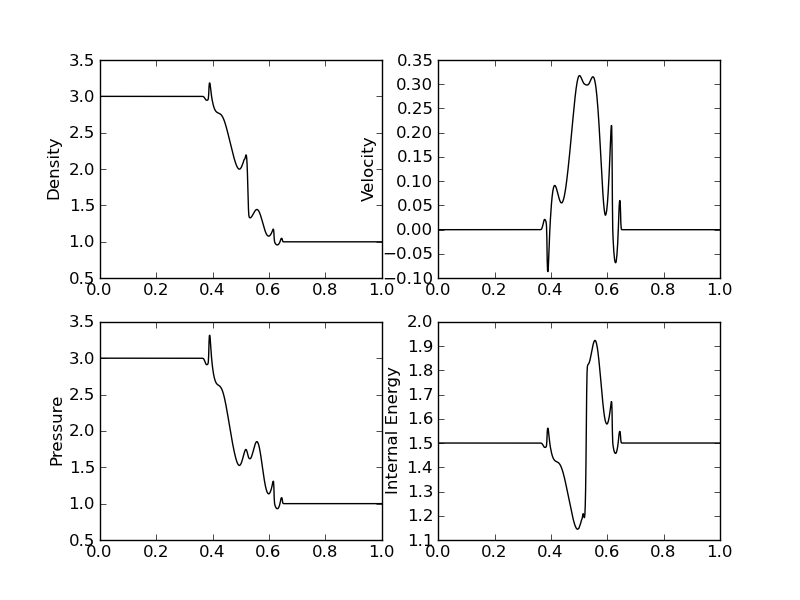
Solution at \(t=0.1\) for Sod-shock problem [s47]. Density (top left), velocity (top right), pressure (bottom left) and internal energy (bottom right). Solutions are significantly different from the homogeneous case and look similar to the two-fluid Riemann solutions.

Conclusions

One conclusion from these series of simulations is that dispersive source terms can cause small-scale features in the solution. To resolve these features sufficient spatial and temporal resolution is needed. Poor spatial resolution can diffuse the oscillations while poor temporal resolution can lead to phase errors. In physical problems (for example multi-fluid plasmas) there is usually some diffusion that is active at small scales and can be important when the gradients change rapidly over a few grid cells. This physical diffusion will wipe out the oscillations from the dispersive sources. Hence, in such cases the resolution of the oscillations might not be so important. However, from a mathematical view-point the numerical schemes need to be accurate enough to resolve such features.