JE11: Benchmarking a finite-element Poisson solver

Contents

• JE11: Benchmarking a finite-element Poisson solver

  • Convergence of 1D solver

    • Dirichlet boundary conditions

    • Dirichlet/Neumann boundary conditions

  • Convergence of high order 1D Poisson solver

    • Convergence of third-order method

    • Convergence of fourth-order method

  • Convergence of 2D solver

  • Convergence of third-order 2D solver

  • Convergence of second-order solver with periodic boundary conditions

  • Conclusions

In this entry I benchmark and test a finite-element method (FEM) Poisson solver. The solver is implemented in Lucee/Gkeyll as the class FemPoissonStructUpdater and solves the equation

\[\nabla^2 \psi = s\]

where \(s\) is the spatially dependent source term. This updater works in 1D, 2D and 3D and is agnostic of the underlying nodal basis functions, which need to be provided separately.

Convergence of 1D solver

In this test the convergence of the 1D solver is tested with an exact solution. The source is chosen to be

\[s(x) = 1-ax^2\]

where \(a=2\). With this the exact solution is

\[\psi(x) = \frac{x^2}{2} - \frac{ax^4}{12} + c_0 x + c_1\]

where \(c_0\) and \(c_1\) are constants of integration.

Dirichlet boundary conditions

For the first test we pick the domain \(x\in [0,1]\) and Dirichlet boundary conditions \(\psi(0)=\psi(1)=0\). With these we get \(c_1=0\) and \(c_0=a/12-1/2\).

The following table shows the errors for the second-order Lobatto scheme with different cell sizes corresponding to 8, 16, 32, and 64 elements and with \(a=2\).

Poisson solver convergence for second-order FEM with Dirichlet boundary conditions

Grid size \(\Delta x\)	Average error	Order	Simulation
\(0.125\)	\(3.797 \times 10^{-4}\)		s77
\(0.0625\)	\(1.01725 \times 10^{-4}\)	1.90	s78
\(0.03125\)	\(2.627\times 10^{-5}\)	1.95	s79
\(0.015625\)	\(6.675726\times 10^{-6}\)	1.98	s80

An example solution with 16 elements is shown below.

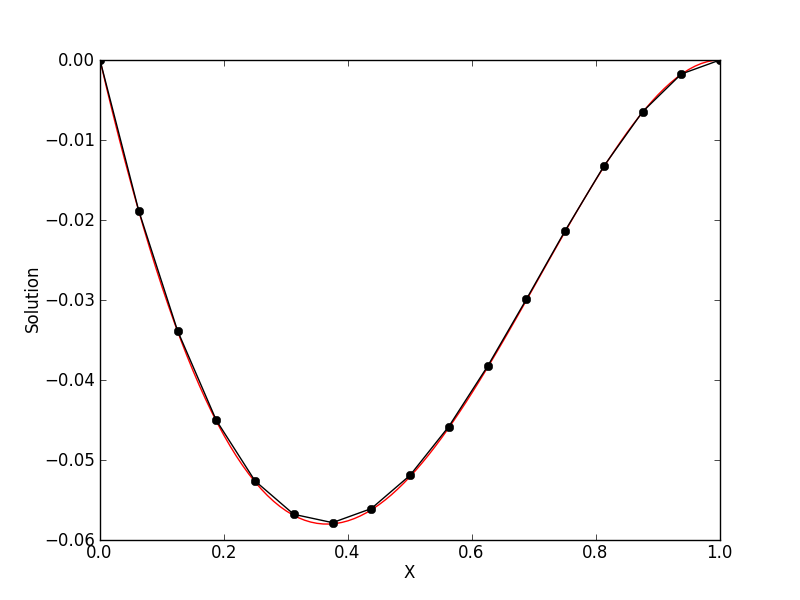
Solution computed with the 1D Poisson finite-element updater (black) compared to the exact solution (red) for 16 elements [s78] and Dirichlet boundary conditions.

Dirichlet/Neumann boundary conditions

For the second test we use Dirichlet and Neumann boundary conditions \({\partial \psi}/{\partial x}=0\) at \(x=0\) and \(\psi(1)=0\). With these we get \(c_0=0\) and \(c_1=a/12-1/2\).

The following table shows the errors for the second-order Lobatto scheme with different cell sizes corresponding to 8, 16, 32, and 64 elements and with \(a=5\).

Poisson solver convergence for second-order FEM with Dirichlet/Neumann boundary conditions

Grid size \(\Delta x\)	Average error	Order	Simulation
\(0.125\)	\(4.20464 \times 10^{-3}\)		s81
\(0.0625\)	\(1.06812 \times 10^{-3}\)	1.98	s82
\(0.03125\)	\(2.69148\times 10^{-4}\)	1.99	s83
\(0.015625\)	\(6.75519\times 10^{-5}\)	1.99	s84

An example solution with 16 elements is shown below.

Solution computed with the 1D Poisson finite-element updater (black) compared to the exact solution (red) for 16 elements [s82] and Neumann boundary conditions on left and Dirichlet boundary conditions on right.

Convergence of high order 1D Poisson solver

In this test the convergence of the 3rd and 4th order 1D solvers is tested with an exact solution. The source is chosen to be

\[s(x) = 1+ax^2+bx^4\]

where \(a=2\) and \(b=-12\). With this the exact solution is

\[\psi(x) = \frac{x^2}{2} + \frac{ax^4}{12} + \frac{bx^6}{30} + c_0 x + c_1\]

where \(c_0\) and \(c_1\) are constants of integration. For the first test we pick the domain \(x\in [0,1]\) and Dirichlet boundary conditions \(\psi(0)=\psi(1)=0\). With these we get \(c_1=0\) and \(c_0=-(1/2+a/12+b/30)\).

Convergence of third-order method

The following table shows the errors for the third-order Lobatto scheme with different cell sizes corresponding to 4, 8, 16, and 32 elements and with \(a=2\).

Poisson solver convergence for third-order FEM with Dirichlet boundary conditions

Grid size \(\Delta x\)	Average error	Order	Simulation
\(0.25\)	\(7.742 \times 10^{-5}\)		s89
\(0.125\)	\(5.397 \times 10^{-6}\)	3.84	s90
\(0.0625\)	\(3.535 \times 10^{-7}\)	3.93	s91
\(0.03125\)	\(2.249\times 10^{-8}\)	3.97	s92

Note that the 3rd order scheme is actually converging with 4th order accuracy. In fact, the 3rd order scheme gives the exact solution when the same source as was used in testing the 2nd order scheme is used.

Convergence of fourth-order method

The following table shows the errors for the fourth-order Lobatto scheme with different cell sizes corresponding to 4, 8, 16, and 32 elements and with \(a=2\).

Poisson solver convergence for fourth-order FEM with Dirichlet boundary conditions

Grid size \(\Delta x\)	Average error	Order	Simulation
\(0.5\)	\(5.536 \times 10^{-5}\)		s93
\(0.25\)	\(1.847 \times 10^{-6}\)	4.90	s94
\(0.125\)	\(5.994 \times 10^{-8}\)	4.94	s95
\(0.0625\)	\(1.910\times 10^{-8}\)	4.97	s96

Convergence of 2D solver

In this test the convergence of the 2D solver is tested with an exact solution. The exact solution is chosen to be

\[\psi(x,y) = f(x;a,c_0,c_1)f(y;b,d_0,d_1)\]

where

\[f(x;a,c_0,c_1) = \frac{x^2}{2} - \frac{ax^4}{12} + c_0 x + c_1\]

Here, I have chosen \(a=2\), \(b=5\), \(c_1=d_0=0\) and \(c_0=a/12-1/2\) and \(d_1=b/12-1/2\). This corresponds to Dirichlet boundary conditions on the left, right and top edge and a Neumann boundary condition on the bottom edge.

The following table shows the errors for the second-order Lobatto scheme with different cell sizes corresponding to \(8\times 8\), \(16\times 16\), \(32\times 32\), and \(64\times 64\) element grids.

Poisson solver convergence for second-order FEM with Dirichlet/Neumann boundary conditions

Grid size \(\Delta x\)	Average error	Order	Simulation
\(0.125\)	\(2.90322 \times 10^{-5}\)		s85
\(0.0625\)	\(7.8699 \times 10^{-6}\)	1.88	s86
\(0.03125\)	\(2.04355\times 10^{-6}\)	1.95	s87
\(0.015625\)	\(5.5524\times 10^{-7}\)	1.89	s88

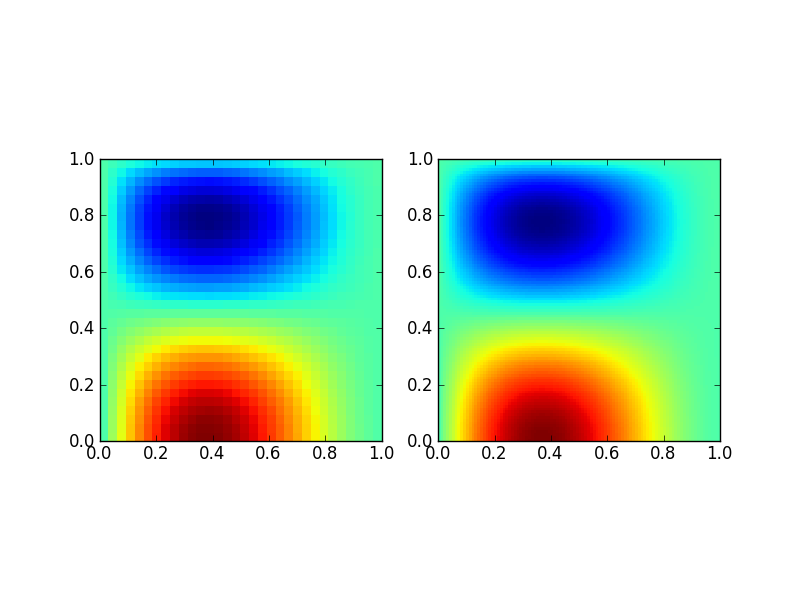
Solution computed with the 2D Poisson finite-element updater (left) compared to the exact solution (right) for \(32\times 32\) element grid [s87]. This corresponds to Dirichlet boundary conditions on the left, right and top edge and a Neumann boundary condition on the bottom edge.

Convergence of third-order 2D solver

In this test the convergence of the third-order 2D solver is tested with an exact solution. The problem setup is the same as used in testing the second-order solver, except using the third-order Serendipity basis functions.

The following table shows the errors for the third-order scheme with different cell sizes corresponding to \(8\times 8\), \(16\times 16\), \(32\times 32\), and \(64\times 64\) element grids.

Poisson solver convergence for third-order FEM with Dirichlet/Neumann boundary conditions

Grid size \(\Delta x\)	Average error	Order	Simulation
\(0.25\)	\(1.156 \times 10^{-5}\)		s97
\(0.125\)	\(8.767 \times 10^{-7}\)	3.72	s98
\(0.0625\)	\(6.043 \times 10^{-8}\)	3.85	s99
\(0.03125\)	\(5.200\times 10^{-9}\)	3.53	s100

The solution converges with greater than third order, as it did for the 1D solver.

Convergence of second-order solver with periodic boundary conditions

The finite-element solver needs significant modification when periodic boundary conditions need to be applied. First, we need to ensure that the source integrated over the domain vanishes, i.e

\[\int_\Omega s(x,y) dx dy = 0\]

To ensure this condition the updater first computes the integrated source and removes that when computing the global source vector.

Further, one needs to carefully build the stiffness matrix to take into account those nodes that the identified with each other due to the periodic boundary conditions. This needs careful book-keeping of local to global index mappings and also accounting for the same periodicity in computing the global source vector. Finally, the stiffness matrix will be singular as with periodic BCs the solution is only determined to an additive constant. To avoid problems with the linear solve one needs to set one location in the domain to an arbitrary value. I have chosen to set the bottom left corner as \(\phi(0,0) = 0\). All these modifications are not trivial and need 2X to 3X more code than needed to just support Dirichlet and/or Neumann boundary conditions.

In this section I test the convergence of the solver using an exact solution given by

\[\phi(x,y) = \frac{1}{N}\sum_{m,n} \left[ a_{mn} \cos(mx) \cos(ny) + b_{mn} \sin(mx) \sin(ny) \right]\]

where \(N\) is a normalizing factor and \(a_{mn}\) and \(b_{mn}\) are specified coefficients. The source corresponding to this solution is

\[s(x,y) = -\frac{1}{N}\sum_{m,n} (m^2+n^2) \left[ a_{mn} \cos(mx) \cos(ny) + b_{mn} \sin(mx) \sin(ny) \right].\]

The domain is \(x \in [0,2\pi]\) and \(y \in [0,2\pi]\). For the other quantities used see the Lua scripts linked below.

The following table shows the errors for the second-order scheme with different cell sizes corresponding to \(32\times 32\), \(64\times 64\) and \(128\times 128\) element grids.

Poisson solver convergence for second-order FEM with periodic boundary conditions

Grid size \(\Delta x\)	Average error	Order	Simulation
\(2\pi/32\)	\(3.718 \times 10^{-3}\)		s101
\(2\pi/64\)	\(9.595 \times 10^{-4}\)	1.95	s102
\(2\pi/128\)	\(2.903 \times 10^{-4}\)	1.72	s103

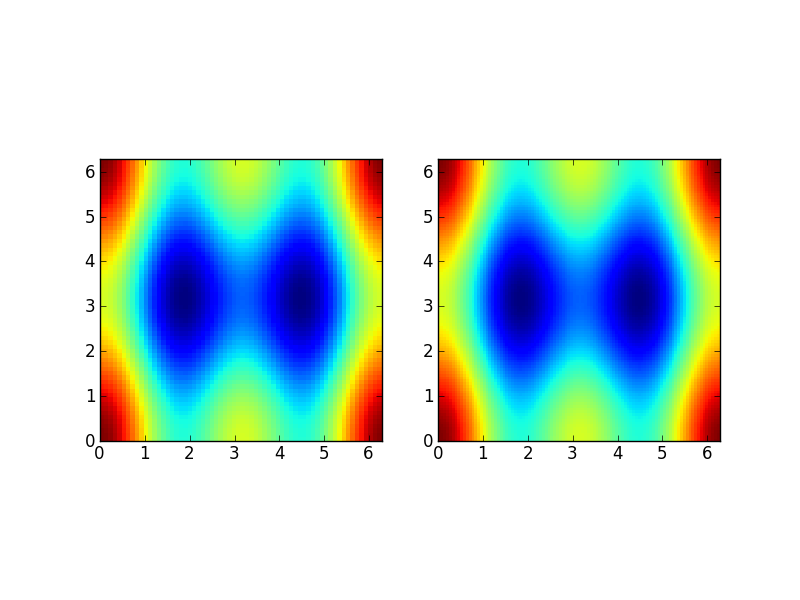
Solution computed with the 2D Poisson finite-element updater with periodic boundary conditions (left) compared to the exact solution (right) for \(64\times 64\) element grid [s102].

Conclusions

With these tests I am reasonably confident that the Poisson finite-element updater works correctly. I have shown the expected convergence behaviour of the 1D and 2D schemes. In 2D I also tested periodic boundary conditions and showed second-order convergence. I have not yet tested the periodic BCs in 1D or the third order 2D periodic BC solver. I will update this entry when I do so.