JE21: Testing a solver for linearized electromagnetic GK equations
Contents
Warning
This note is incomplete.
I need to put full dimensional EM equations.
Put dispersion relations and link to Python code.
I may need to redo some plots, as perhaps I have some normalizations confused.
There is also some notational confusion between \(f(z,p_\parallel,t)\) and \(f(z,v_\parallel,t)\).
In this note I test a solver for the linearized electromagentic gyrokinetic equations. This system is described by the Vlasov equation for the electrons
where \(f(z,p_\parallel,t)\) is the electron distribution function 1 and the Hamiltonian is given by
where \(A_\parallel\) is the parallel magnetic potential and \(\phi\) is the electrostatic potential, \(m_e\) is the electron mass and \(q_e = -|e|\) is the electron charge. The ions are assumed to be stationary.
Normalized linear system
To linearize the system we first linearize the Hamiltonian around a field-free equilibirum to write
Here \(H\) is the linearized Hamiltonian. The zeroth-order Hamiltonian describes free-streaming
and the first-order Hamiltonian describes motion of the perturbations
Writing \(f(z,p_\parallel,t) = f_0(z,p_\parallel) + f_1(z,p_\parallel,t)\) the linearized Vlasov equation is given by
Note that only the zeroth-order Hamiltonian acts on the perturbed distribution, while the full linearized Hamiltonian acts on the equilibirum distribution. The linearized electromagnetic field equations become: Ampere’s law
and the GK Poisson equation
where \(q_i = Z_i |e|\) is ion charge, and \(v_\parallel = (p_\parallel-q_e A_\parallel)/m_e\) is the parallel velocity.
We normalize the equations as follows. We pick \(q_e=-1\), \(m_e=1\) and \(v_{te}=1\). To simpify the notation we now use \(w\) as the momentum space coordinate. The form of normalized Vlasov equation remains unchanged, with the Hamiltonians given by \(H_0 = w^2/2\) and
Note that in this normalization, effectively \(k_\perp^2\) is normalized to \(Z_i\rho_i^2\) and \(\hat{\beta} \equiv (\beta_e/2) m_i/m_e\), where \(\beta_e\) is the electron plasma-beta. In these units, the Alfven speed is \(v_A=1/\sqrt{\hat{\beta}}\). The normalized equilibrium distribution is \(f_0 = e^{-w^2/2}/\sqrt{2\pi}\).
The EM equations become
Note that the normalized system is identical to the one described in the appendix of Belli and Hammett 2005 2.
To solve this system with Gkeyll we use two Poisson Bracket updaters, one acting on the perturbed distribution and the other acting on the equilibrium distribution. The perturbed Hamiltonian is computed from the EM fields, after they are projected onto continious basis functions.
Note
In the implementation used here, the Hamiltonian is computed by evaluating it at the nodes of the nodal basis functions. This ensures continuity, however, is not an \(L_2\) fit onto the continuous basis functions. This could results in a small loss in accuracy, although total energy will still be conserved.
Electron acoustic waves
We first look at the electrostatic limit, i.e. set \(\hat{\beta}=0\). In this limit the system supports electron acoustic waves, which are increasingly Landau damped as \(k_\perp^2\) increases.
The first set of simulations were performed with a piece-wise first-order polynomial basis functions on a \(16\times 32\) grid. The second set of simulations were performed on the same grid, except using piece-wise second-order polynomials.
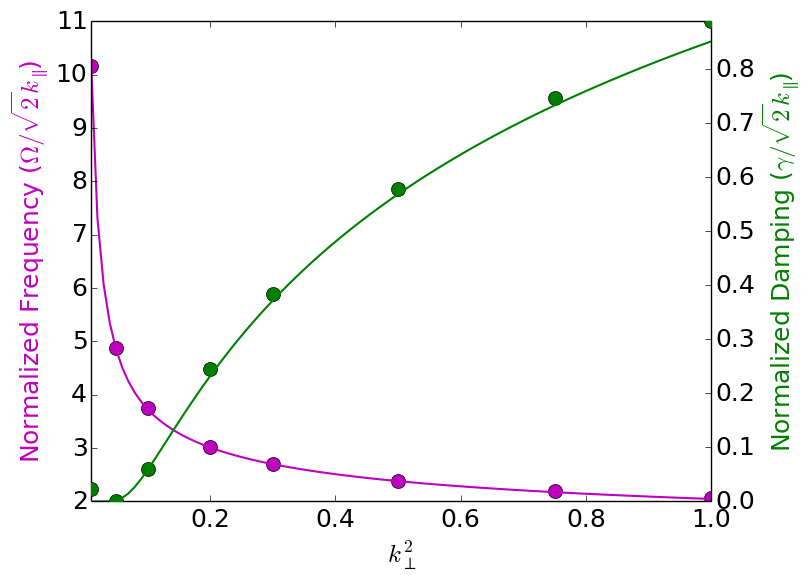
Frequency (magenta, left axis) and damping (green, right axis) for electron acoustic waves. Solid dots are simulation results on a \(16\times 32\) grid with piece-wise first-order polynomial basis functions. Note that the resolution is rather coarse, and the discretization errors are particularly noticeable in the damping rates. In these simulations \(\hat{\beta}=0.0\), and \(k_\perp^2=0.01,\ldots,1.0\). See simulations [347] to [s354] for details.
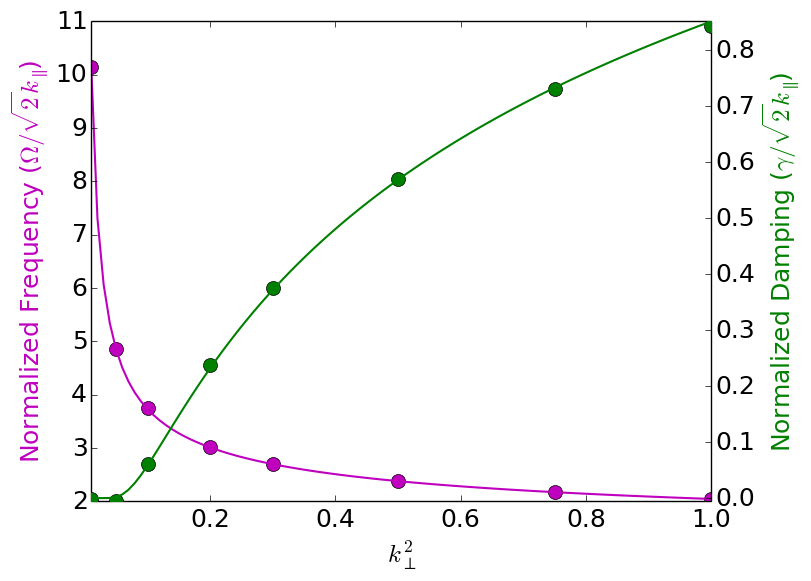
Same as the previous figure, except using piece-wise second order polynomial basis functions. The damping rates are much better predicted than in the first-order polynomial case, however, the simulations take twice as long. See simulations [s355] to [s362] for details.
Shear Kinetic Alfven waves
In the next set of calculations, we look at the case in which EM terms are included, i.e. \(\hat{\beta}>0.0\). In this case the system supports shear kinetic Alfven waves (KAWs), which asymptote to undamped waves as \(k_\perp\rightarrow 0\).
Case when \(k_\perp^2=0.1\)
For first set of tests I hold \(k_\perp^2=0.1\) and vary \(\hat{\beta}=0.1,\ldots,10.0\). For all simulations piece-wise second-order basis functions on a grid of \(16\times 32\) were used. One of the reasons to use a second-order polynomial basis functions is that it delays recurrence issues, rather severe in the lower-order basis function case. Eventually, we will implement a hyper-collision term to damp out the recurrence, but this has not been tested yet.
The results are shown in the following figure.

Frequency (magenta, left axis) and damping (green, right axis) for shear kinetic Alfven waves (KAWs). Solid dots are simulation results on a \(16\times 32\) grid with piece-wise second-order polynomial basis functions. Note that the damping rates do not agree very well for the \(\hat{\beta}=10.0\) case. See simulations [s363] to [s369] for details.
Case when \(k_\perp^2=0.05\)
In this set of tests I hold \(k_\perp^2=0.05\) and vary \(\hat{\beta}=0.1,\ldots,10.0\). All other parameters are the same as for the \(k_\perp^2=0.1\) case.
The results are shown in the following figure.
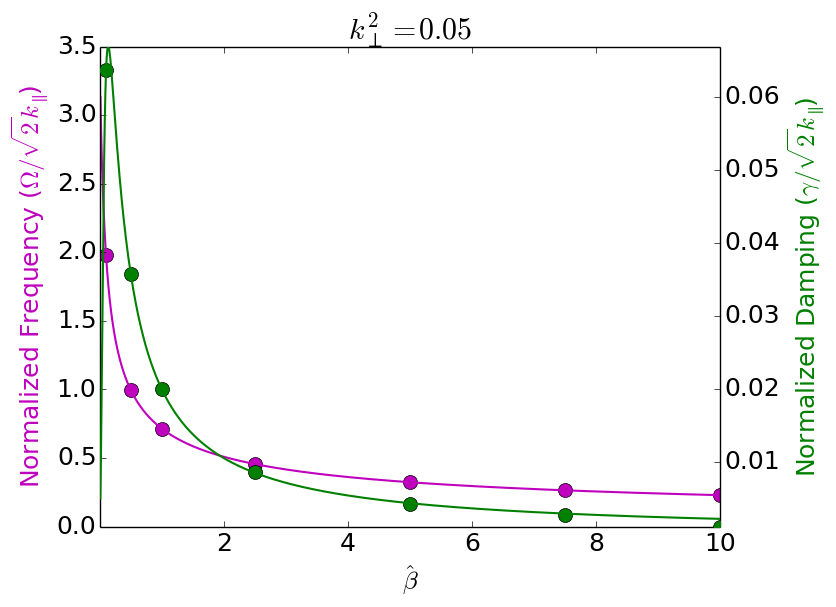
Frequency (magenta, left axis) and damping (green, right axis) for shear kinetic Alfven waves (KAWs). Solid dots are simulation results on a \(16\times 32\) grid with piece-wise second-order polynomial basis functions. See simulations [s370] to [s370] for details.
Case when \(k_\perp^2=0.01\)
In this set of tests I hold \(k_\perp^2=0.01\) and vary \(\hat{\beta}=0.1,\ldots,10.0\). All other parameters are the same as for the \(k_\perp^2=0.1\) case.
The results are shown in the following figure.
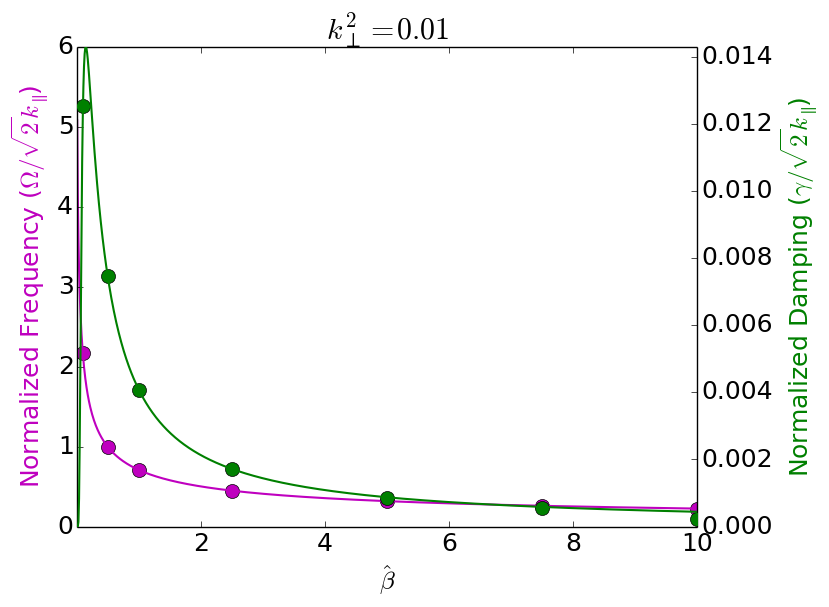
Frequency (magenta, left axis) and damping (green, right axis) for shear kinetic Alfven waves (KAWs). Solid dots are simulation results on a \(16\times 32\) grid with piece-wise second-order polynomial basis functions. See simulations [s370] to [s370] for details.
Case when \(\hat{\beta}=10\)
In the next set of tests \(\hat{\beta}=10\), while \(k_\perp^2=10^{-4},\ldots,1.0\). A grid of \(16\times 32\) cells, with piece-wise second-order polynomial basis functions were used. For the case \(k_\perp^2=10^{-4}\), a fixed time-step \(\Delta t = 10^{-3}\) was used to avoid continuous adjustments from the Poisson Bracket algorithm. For all other tests the largest time-step allowed by the CFL condition was used.
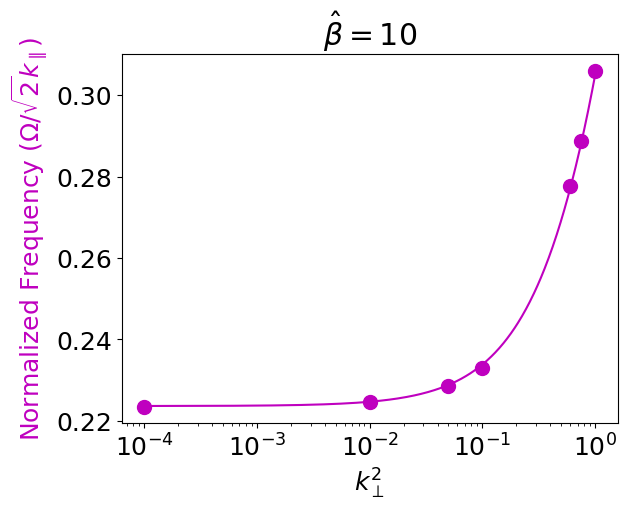
Frequency for shear kinetic Alfven waves (KAWs), with fixed \(\hat{\beta}=10\). Solid dots are simulation results on a \(16\times 32\) grid with piece-wise second-order polynomial basis functions. Gkeyll predicts the frequency to at least two significant figures in each case.
Comparison with nonlinear solver
In this section, I test a solver for the full nonlinear electromagnetic gyrokinetic equations. Only the electron dynamics is retained, i.e. the ions are assumed to be stationary. The evolution equation is
where, now the Hamiltonian is given by (1). The field equations remain unchanged. The current implementation in Gkeyll evolves only the perturbed distribution function, however the Poisson Bracket operator is now applied to the total distribution and the nonlinear Hamiltonian.
The follow table compares the values obtained for the frequencies for the \(\beta=10.0\) case and various values of \(k_\perp\).
\(k_\perp^2\) |
Linear Code |
Nonlinear Code |
Exact |
|---|---|---|---|
\(1 \times 10^{-2}\) |
0.22465 |
0.22468 |
0.22466 |
\(5\times 10^{-2}\) |
0.22856 |
0.22856 |
0.22879 |
This test shows that both the nonlinear and linear codes give the same answer to two significant figures, showing that there is no fundamental problem with the DG algorithm for nonlinear EM/GKE.
- 1
The distribution function is for the guiding centers. However, in this note the zero gyro-radius approximation is used for the electrons, and the particle and guiding center distributions coincide.
- 2
Belli, E. A., & Hammett, G. W. “A numerical instability in an ADI algorithm for gyrokinetics”, Computer Physics Communications, 172 (2), 119–132, 2005. doi:10.1016/j.cpc.2005.06.007