JE28: Some tests for Boltzmann-BGK equations

Note

This note is written with Petr Cagas, a graduate student at Virginia Tech. Petr wrote the code to compute a Maxwellian from moments. This updater at present does not conserve the moments. I.e. moments computed from the Maxwellian won’t exactly match the moments used to compute the Maxwellian. We hope to fix this soon.

Contents

• JE28: Some tests for Boltzmann-BGK equations

  • Introduction

  • Notes on algorithm: positivity and asymptotic preservation

  • Test Problems

    • Problem 1: Relaxation of step function to Maxwellian

    • Problem 2: Sod-shock problem

    • Problem 3: Counter propagating jets

  • Conclusion

  • References

Introduction

Gkeyll includes the ability to incorporate (as of this writing) both a BGK and a Lenard-Bernstein (LB) collision operator. The LB operator is modified to ensure momentum and energy conservation. In this note, I test the BGK operator in the context of kinetic simulations of neutral gas dynamics.

The neutral gas dynamics system, with the BGK operator, is given by

\[\frac{\partial f}{\partial t} + v \frac{\partial f}{\partial x} = \nu (f_M - f)\]

where \(f_M\) is the Maxwellian distribution computed from the moments of \(f(x,v,t)\):

\[f_M(x,v,t) = \frac{n}{\sqrt{2\pi v_{th}^2}} \exp(-(v-u)^2/2 v_{th}^2)\]

where

\[\begin{split}n \equiv \int f(x,v,t) \thinspace dv \\ nu \equiv \int v f(x,v,t) \thinspace dv \\ nu^2 + n v_{th}^2 \equiv \int v^2 f(x,v,t) \thinspace dv\end{split}\]

The above equations are written in 1X/1V, however, the code works in higher dimensions.

Notes on algorithm: positivity and asymptotic preservation

The are two major issues with algorithms for Boltzmann type equations (i.e. with collisions) which one needs to deal with. The first, is to ensure that the distribution function remains positive, and second, to ensure that the time-step in the very high collisionality regime is not dominated by the collision frequency.

Gkeyll’s current algorithm for evolving the distribution function does not maintain positivity. However, a positivity “fix” (which maintains particle conservation) has been implemented, and can applied as a filter step. This positivity fix, although conservative and easy to use, is not very good as it often reduces the order of the scheme. Better schemes will be implemented in the future.

Its clear from the form of the BGK operator, that for \(\nu \rightarrow \infty\), the collisional sources become very stiff. In this fluid regime the time-step restriction from the collisions become more severe than the explicit time-step from the thermal velocity. Hence, to avoid taking a small time-step, an asymptotic preserving (AP) method needs to be implemented 1. (Note that to achieve AP property we need to ensure also that the spatial scheme is AP. This is naturally the case for the Gkeyll kinetic solver, which asymptotes to a kinetic-Riemann solver based fluid solver in the fluid limit). As far as can be determined, this can be done from the Lua script without any new C++ code. We hope to do this soon.

Test Problems

Problem 1: Relaxation of step function to Maxwellian

In this test the relaxation of an initial non-Maxwellian distribution function to Maxwellian (due to collisions) is studied. The initial distribution function is a step-function in velocity space:

\[\begin{split}f(x,v,t) &= \frac{1}{2v_0} \quad &|v| < v_0 \\ &= 0 \quad &|v| > v_0\end{split}\]

where \(v_0 = 3 v_{th}/2\). 32 cells are used in velocity space, with piece-wise quadratic Serendipity basis elements. The simulation is run to steady-state, and the resulting Maxwellian compared with the exact solution. Note that as the BGK operator (as all collision operators) conserves density, momentum and energy, we can easily calculate the expected solution (for comparison) from the parameters of the selected initial distribution function. The results are shown in the figure below. As can be seen, the steady-state solution matches the exact solution very well.

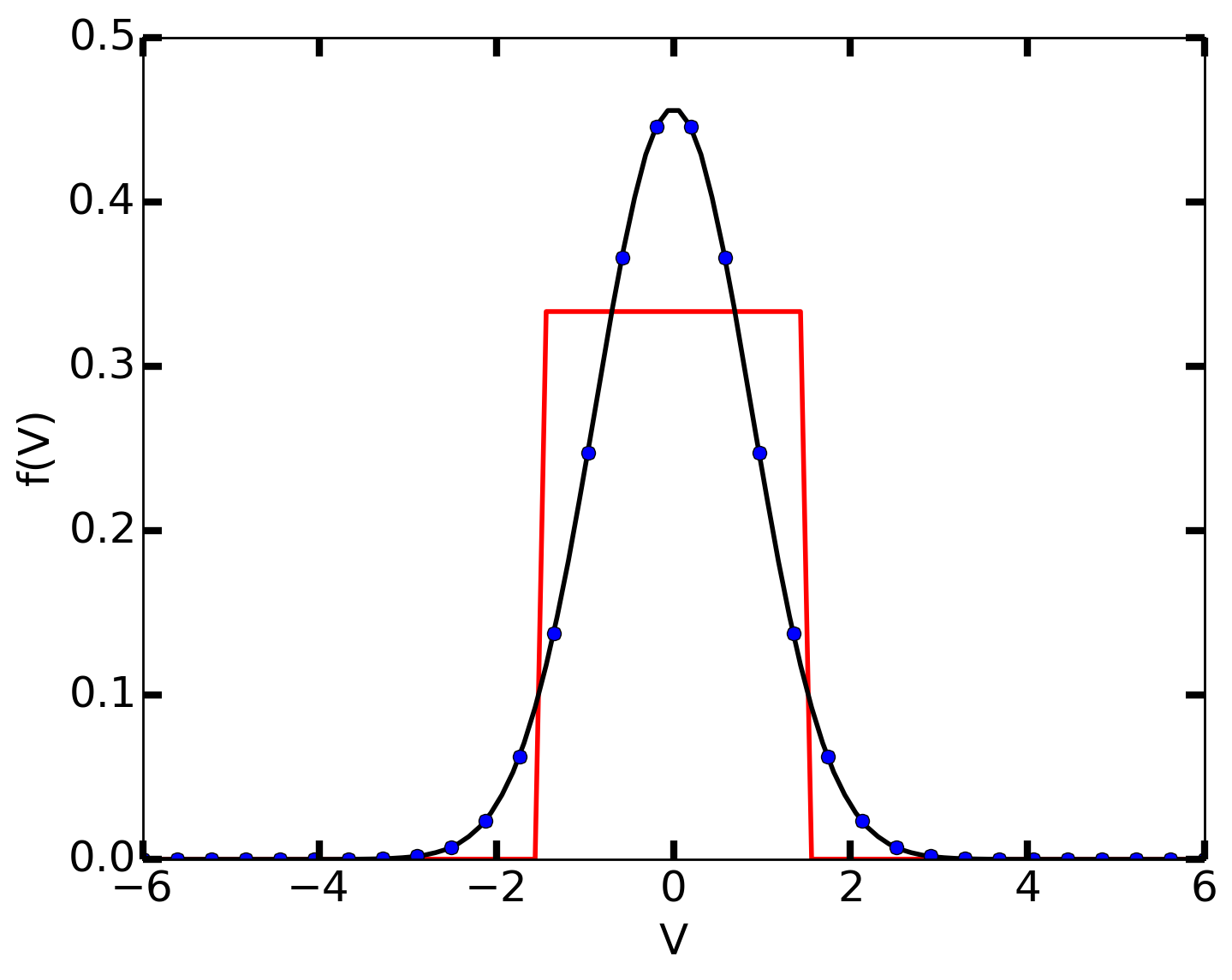
Relaxation of an initial step-function distribution function (red-line) to a Maxwellian. Black line is the numerical solution, while blue dots are the exact solution computed from the moments of the initial condition. See [s1] for input file.

Problem 2: Sod-shock problem

This problem is the generalization of the classical Sod-shock to the Boltzmann-BGK system. The initial conditions are

\[\begin{split}\left[ \begin{matrix} \rho_l \\ u_l \\ p_l \end{matrix} \right] = \left[ \begin{matrix} 1 \\ 0.0 \\ 1.0 \end{matrix} \right], \qquad \left[ \begin{matrix} \rho_r \\ u_r \\ p_r \end{matrix} \right] = \left[ \begin{matrix} 0.125 \\ 0.0 \\ 0.1 \end{matrix} \right].\end{split}\]

For a 1D/1V system, the thermal velocity needs to be computed as \(p=n v_{th}^2\), indicating a gas adiabatic constant of \(\gamma=3\). (The internal energy is \(p/(\gamma-1) = n v_{th}^2/2\), which means \(\gamma=3\)).

The simulations were run with 128 spatial cells, and 32 velocity cells, with piecewise polynomial order 2 elements, and to \(t=0.1\). The Knudsen number (\(\mathrm{Kn} = \lambda_\textrm{mfp}/L\)) is varied from \(1/10\), \(1/100\) and \(1/1000\). In the first case, the gas is collisionless (on the time-scale of the simulation), and in the last case, the gas is highly collisional. Hence, the solution should match (approximately) the solution from (Navier-Stokes) Euler equations.

In the following figures, the results with various Knudsen numbers are shown, as well the exact solution of the Euler equations for the same parameters. Note that the Euler equations represent the inviscid limit of the Boltzmann equation, and hence even in high collisionality regime won’t match the kinetic results exactly. In fact, the high collisionality results would be better compared to a Navier-Stokes solution, with transport parameters derived from the BGK operator (rather than the Boltzmann collision operator).

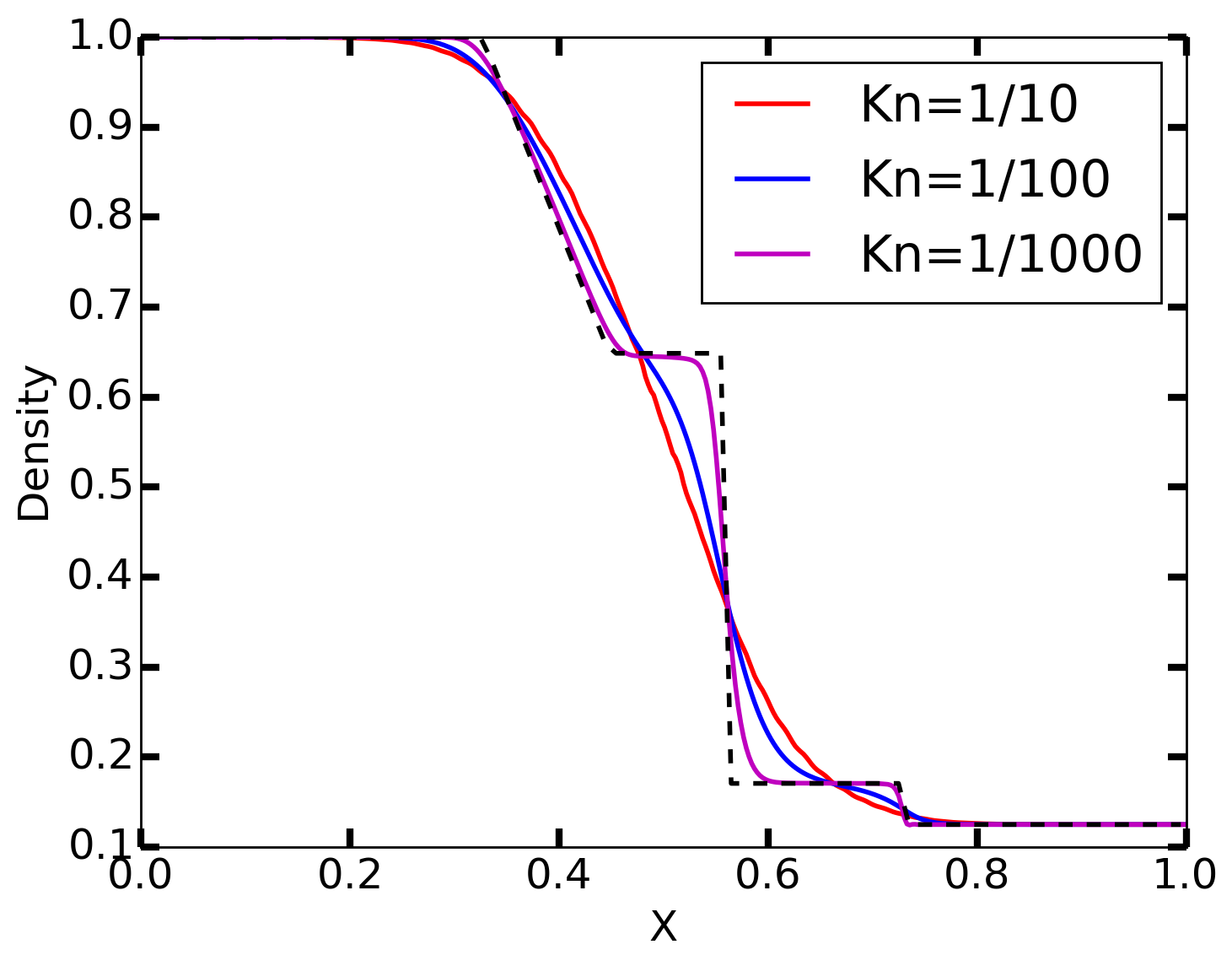
Density from Sod-shock problem for \(\mathrm{Kn}=1/10\) (red) [s2], \(\mathrm{Kn}=1/100\) (blue) [s3], and \(\mathrm{Kn}=1/1000\) (magenta) [s4]. The black dashed line shows the exact solution from the Euler equation.

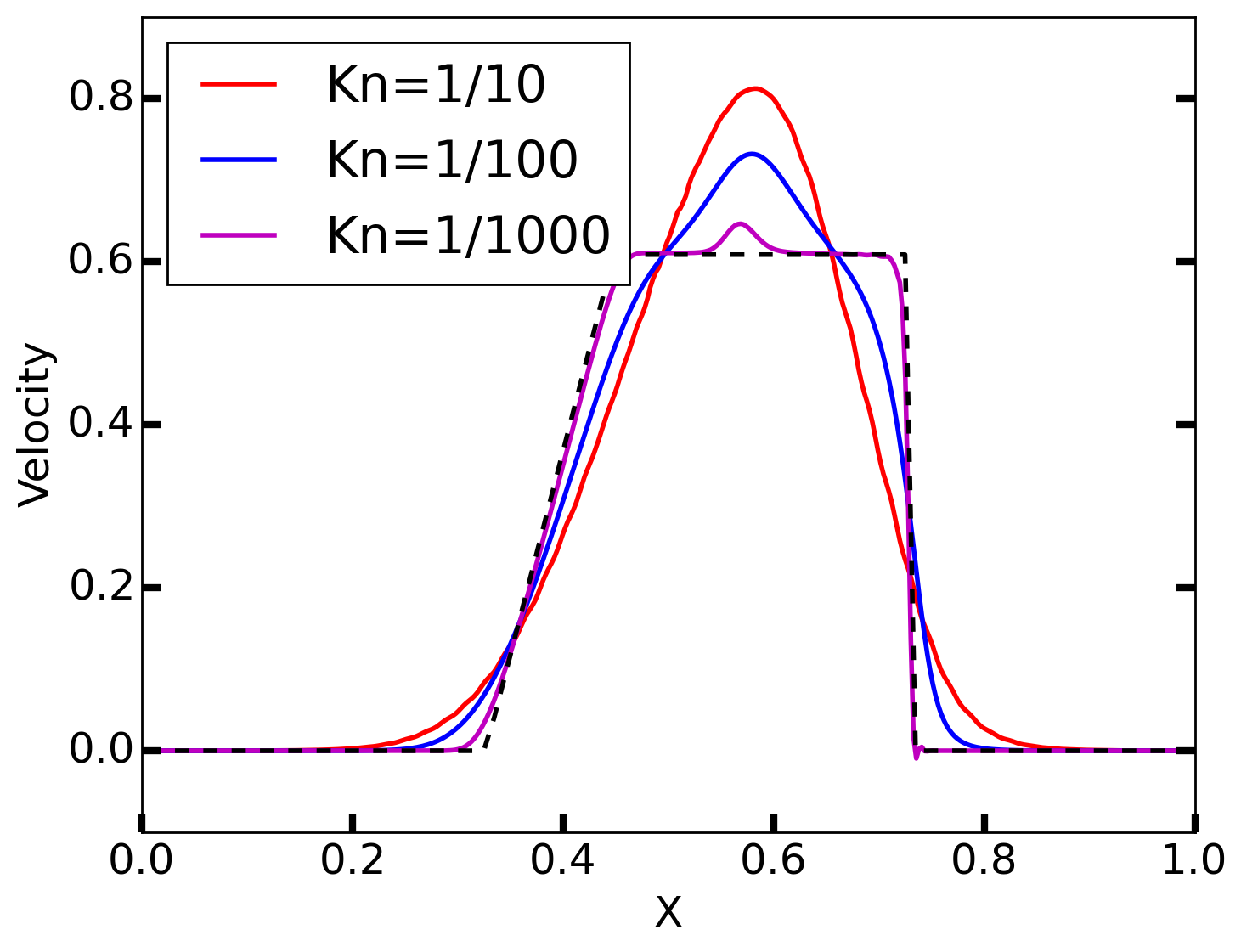
Velocity from Sod-shock problem for \(\mathrm{Kn}=1/10\) (red) [s2], \(\mathrm{Kn}=1/100\) (blue) [s3], and \(\mathrm{Kn}=1/1000\) (magenta) [s4]. The black dashed line shows the exact solution from the Euler equation.

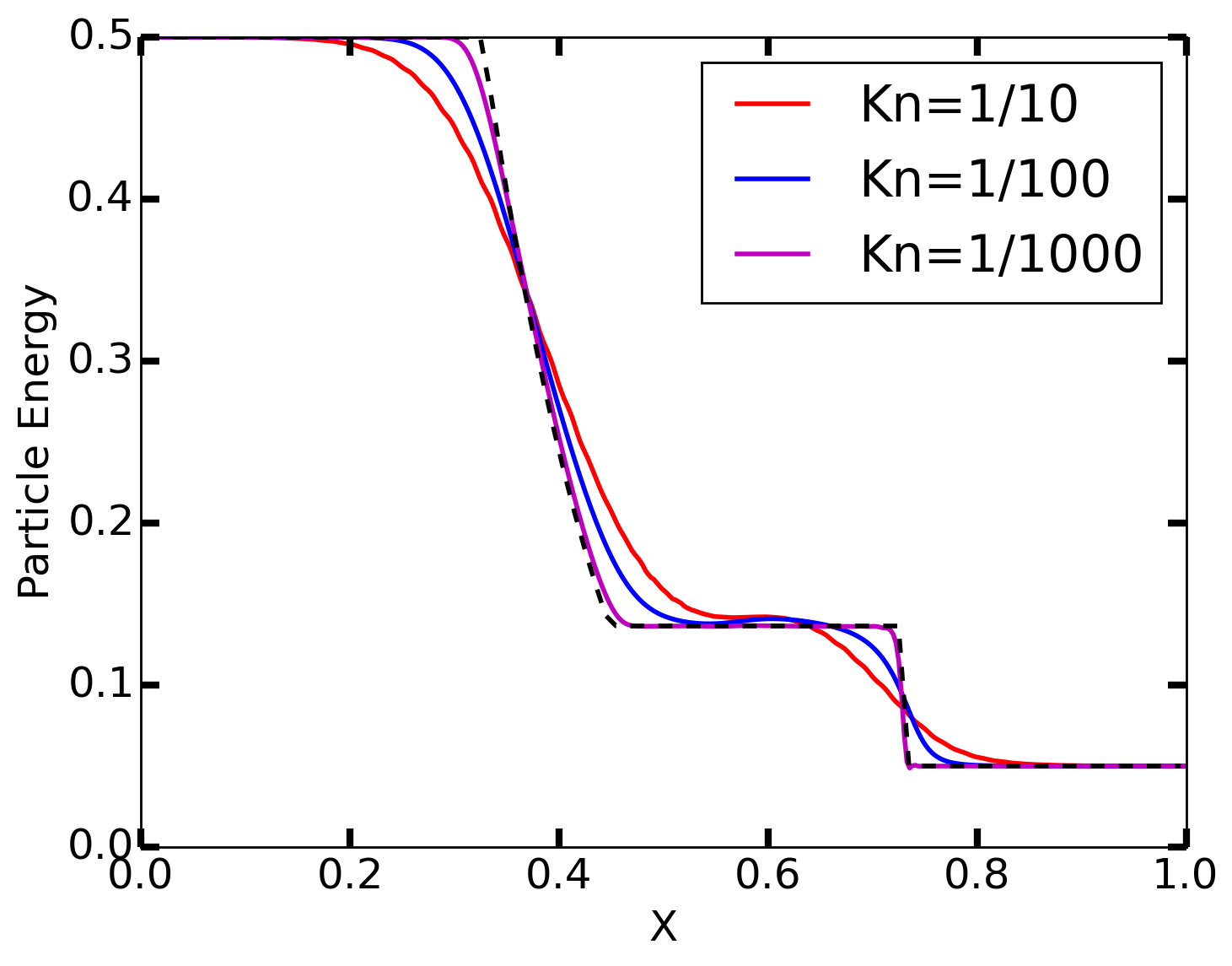
Internal energy (\(n v_{th}^2/2 = p/(\gamma-1)\)) from Sod-shock problem for \(\mathrm{Kn}=1/10\) (red) [s2], \(\mathrm{Kn}=1/100\) (blue) [s3], and \(\mathrm{Kn}=1/1000\) (magenta) [s4]. The black dashed line shows the exact solution from the Euler equation.

Problem 3: Counter propagating jets

In this problem two counter propagating jets interact, creating quasi-steady shocks. The initial conditions are

\[\begin{split}\left[ \begin{matrix} \rho_l \\ u_l \\ p_l \end{matrix} \right] = \left[ \begin{matrix} 1 \\ 0.75 \\ 1.0 \end{matrix} \right], \qquad \left[ \begin{matrix} \rho_r \\ u_r \\ p_r \end{matrix} \right] = \left[ \begin{matrix} 0.125 \\ -0.75 \\ 0.75 \end{matrix} \right].\end{split}\]

Note that the jets are not symmetrical: the jet propagating to the left has a lower pressure. The propagating shock fronts are steady-state (in the frame of the shock), and it should be possible to compare with kinetic shock theory. The simulations were run with 128 spatial cells, and 32 velocity cells, with piecewise polynomial order 2 elements, and to \(t=0.15\). The Knudsen numbers we set to \(1/100\) and \(1/1000\). Results are shown below.

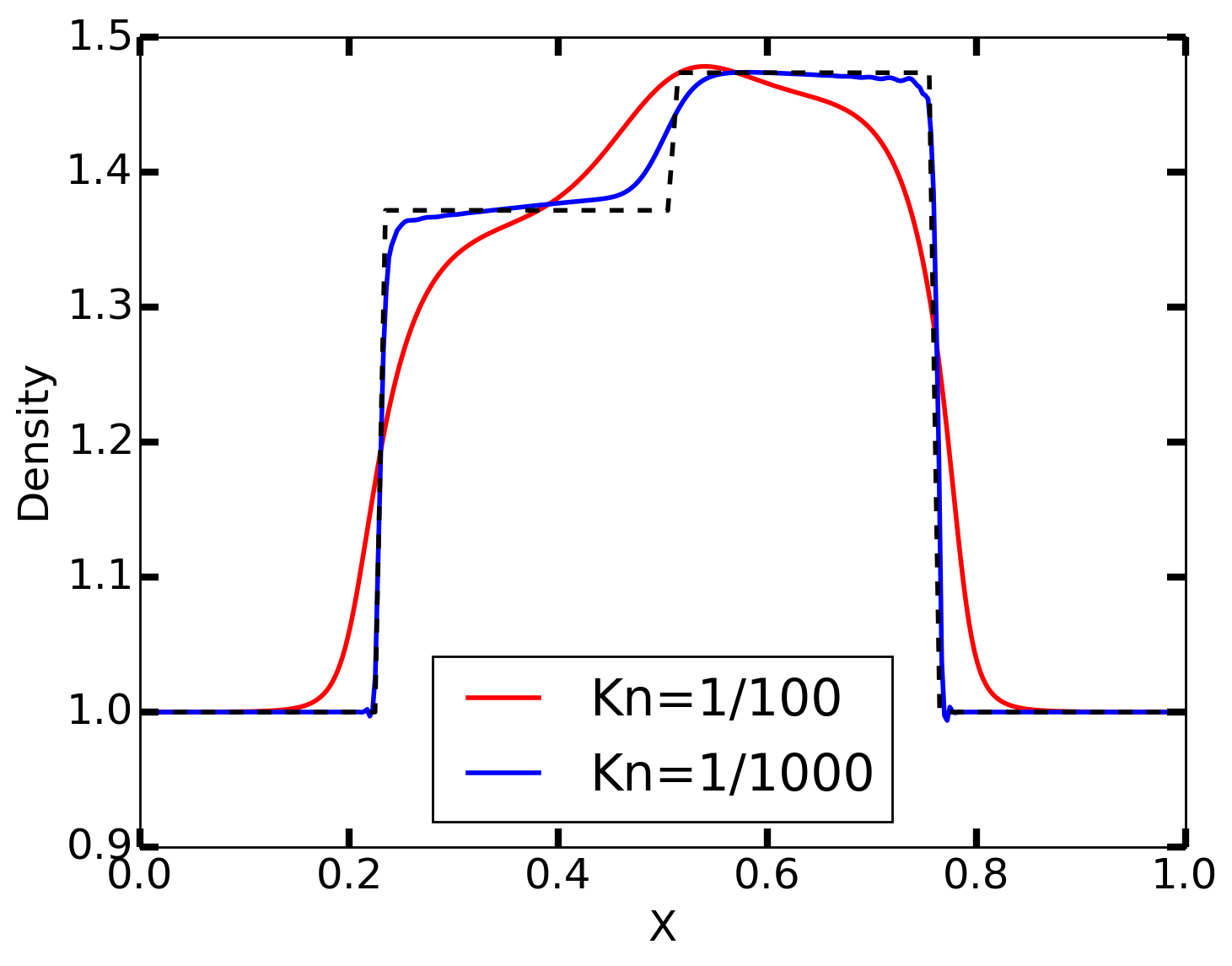
Density from jets problem for \(\mathrm{Kn}=1/100\) (red) [s5] and \(\mathrm{Kn}=1/1000\) (blue) [s6]. The black dashed line shows the exact solution from the Euler equation.

Velocity from jets problem for \(\mathrm{Kn}=1/100\) (red) [s5] and \(\mathrm{Kn}=1/1000\) (blue) [s6]. The black dashed line shows the exact solution from the Euler equation.

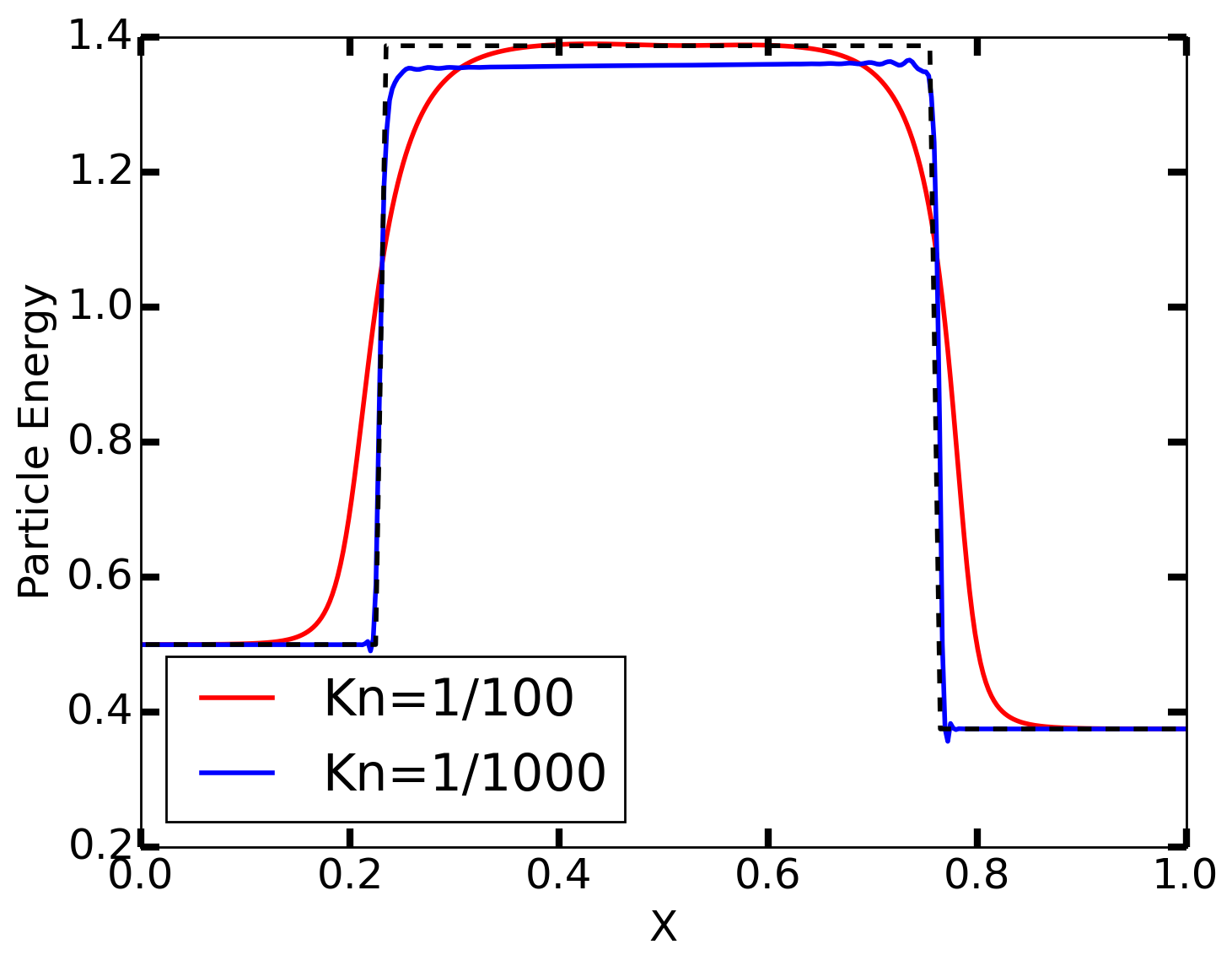
Internal energy (\(n v_{th}^2/2 = p/(\gamma-1)\)) from jets problem for \(\mathrm{Kn}=1/100\) (red) [s5] and \(\mathrm{Kn}=1/1000\) (blue) [s6]. The black dashed line shows the exact solution from the Euler equation. I am not completely sure why the high collisionality solution (blue) converges to a lower energy level than the Euler solution.

Conclusion

Some basic tests for the Boltzmann-BGK collision operator have been presented. From these tests it seems that the collisional kinetic physics is being captured correctly. Issues of positivity and asymptotic preservation remain, but these will be fixed in the near future.

References

1

Pareschi, L., & Russo, G.. “Implicit-explicit Runge-Kutta schemes and applications to hyperbolic systems with relaxation”. arXiv:1009.2757.