JE26: Benchmarking a discontinuous Galerkin algorithm for Maxwell equations

Contents

• JE26: Benchmarking a discontinuous Galerkin algorithm for Maxwell equations

  • Problem 1: Exact plane-wave solutions

    • Convergence of 1D schemes

    • Convergence of 2D schemes

  • Problem 2: Electromagnetic pulse in a box

  • Conclusion

In this note I benchmark a nodal discontinuous Galerkin solver for Maxwell equations. This solver will be used as part of the Vlasov-Maxwell and multi-fluid equations. For notes on Maxwell equations and divergence cleaning, please see JE6.

For Maxwell equations, it can be shown that the spatial operator of the DG scheme conserves the electromagnetic (EM) energy exactly when using central fluxes. However, with upwinding the EM energy decays monotonically. Note that the time-stepping scheme (in this case a SSP-RK3 scheme) will add some dissipation, and hence the fully discrete scheme will decay the energy (not necessarily monotonically), independent of numerical fluxes used.

Gkeyll at present (as of May 19th 2015) has polynomial order 1 and 2 serendipity elements, and arbitrary order Lagrange tensor elements. In the near future we hope to have higher order serendipity element as well as other basis sets in which the number of degrees-of-freedom (DOFs) are minimized.

The nodal DG solver works in 1D, 2D and 3D, but only 1D and 2D studies are shown below.

Note

A note on plotting. The DG scheme yields expansion coefficients in basis functions in each cell. Hence, I project the solution onto a finer mesh before plotting. For a order \(p\) basis, I project on \(p+1\) sub-cells (in each direction). Note that this may actually be under-projection as perhaps a more accurate picture may be obtained by projecting on \(2p+1\) sub-cells (in each direction). For this, I would need to extend my plotting script, which I am too lazy to do at present.

Problem 1: Exact plane-wave solutions

To test the convergence of the scheme, we can use a general wave solution on a periodic domain. Let \(\mathbf{k} = 2\pi(k,l,m)/L\) be a wave-vector such that \(|\mathbf{k}|\ne 0\). Let \(\mathbf{n}\) be a non-zero vector such that \(\mathbf{k}\cdot\mathbf{n} = 0\). Then, a general periodic solution of Maxwell equations on a domain \(L\times L\times L\) is

\[\begin{split}\mathbf{E} &= E_0 \cos(\mathbf{k}\cdot\mathbf{x} - |\mathbf{k}|c t + \delta)\hat{\mathbf{n}} \\ \mathbf{B} &= E_0\sqrt{\mu_0\epsilon_0} \cos(\mathbf{k}\cdot\mathbf{x} - |\mathbf{k}|c t + \delta)\hat{\mathbf{k}}\times\hat{\mathbf{n}}\end{split}\]

where \(\hat{\mathbf{n}}\) and \(\hat{\mathbf{k}}\) are unit vectors. We can use this solution to generate 1D and 2D initial conditions that can be used to test the convergence of the scheme.

Errors in the L1 norm of the solution of \(E_z\) are computed. These correspond to computing the errors in the cell averages. Let \(E_{z0}\) be the initial conditions, projected on the selected basis functions. Then, the errors are computed as

\[\epsilon = \sum_j \left|\int_{I_j} E_z - E_{z0} \thinspace dx dy \right|\]

where the sum is performed over all cells. Other norms can also be used, and I intend to do this at some point. For example, the L2 norm may be a better measure, as it would also account for the convergence of higher order moments of the solution.

Convergence of 1D schemes

For this problem I pick \(\mathbf{k} = 2\pi(2,0,0)/L\), with \(L=1\). The simulation is run for one period, i.e. to \(t=2\pi|\mathbf{k}|c\). Physical values of speed of light and other physical constants are used. To study spatial convergence, the time-step is kept constant, and the number of cells are doubled.

Results are shown below for various polynomial orders and basis functions.

Serendipity polynomial order 1

Grid size \(\Delta x\)	Average error	Order	Simulation
\(0.025\)	\(5.373\times 10^{-3}\)		s1
\(0.0125\)	\(5.794\times 10^{-4}\)	\(3.2\)	s2
\(0.00625\)	\(6.6596\times 10^{-5}\)	\(3.1\)	s3

Serendipity polynomial order 2

Grid size \(\Delta x\)	Average error	Order	Simulation
\(0.1\)	\(9.639\times 10^{-3}\)		s4
\(0.05\)	\(2.8299\times 10^{-4}\)	\(5.1\)	s5
\(0.025\)	\(1.17\times 10^{-5}\)	\(4.6\)	s6

Lagrange tensor, polynomial order 3

Grid size \(\Delta x\)	Average error	Order	Simulation
\(0.25\)	\(5.186\times 10^{-2}\)		s8
\(0.125\)	\(8.9183\times 10^{-5}\)	\(9.1\)	s9
\(0.0625\)	\(3.3212\times 10^{-5}\)	\(1.45\)	s10

Discussion Note that the DG scheme with serendipity basis converges faster than \(p+1\), and seem to converge as \(2p+1\). The Lagrange tensor solution converges even faster, however, then levels off, probably because the errors are too small to measure accurately. Also, note that in general going to higher order reduces the error dramatically, even on much coarser meshes.

Convergence of 2D schemes

For this problem I pick \(\mathbf{k} = 2\pi(2,2,0)/L\), with \(L=1\). The simulation is run for one period, i.e. to \(t=2\pi|\mathbf{k}|c\). The wave propagates diagonally, testing propagation of waves transverse to the grid. Equal number of cells are used in each direction.

Results are shown below for various polynomial orders and basis functions.

Serendipity polynomial order 1

Grid size \(\Delta x\)	Average error	Order	Simulation
\(0.05\)	\(1.2\times 10^{-1}\)		s15
\(0.025\)	\(1.22\times 10^{-2}\)	\(3.3\)	s16
\(0.0125\)	\(1.25\times 10^{-3}\)	\(3.3\)	s17

Serendipity polynomial order 2

Grid size \(\Delta x\)	Average error	Order	Simulation
\(0.1\)	\(3.48\times 10^{-2}\)		s18
\(0.05\)	\(1.065\times 10^{-3}\)	\(5.0\)	s19
\(0.025\)	\(4.312\times 10^{-5}\)	\(4.6\)	s20

Example solutions with polynomial order 1 on grid \(40\times 40\) and polyorder 2 on grid \(20\times 20\) are shown below.

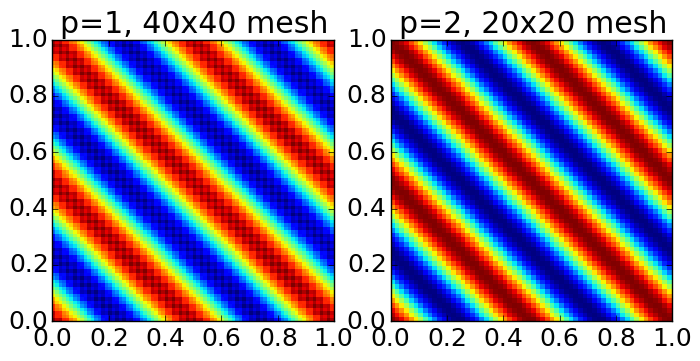
Solution (\(E_z\)) computed with polynomial order 1 on grid \(40\times 40\) grid (left) [s16] and polyorder 2 on grid \(20\times 20\) (right) [s19]. The piecewise quadratic scheme is more accurate and runs faster than the piecewise linear scheme. This is also evident from the errors shown in the tables above.

Problem 2: Electromagnetic pulse in a box

In this problem we initialize a Gaussian pulse in a metal box and evolve the resulting fields. The electric field is initialized with

\[E_z = e^{-\beta r^2}\]

where \(r = \sqrt{x^2 + y^2}\), on a square domain \([-1,1] \times [-1,1]\), with \(\beta = 25\). Piecewise linear serendipity element on a \(32\times 32\) grid, quadratic serendipity elements on a \(16\times 16\) grid and piecewise cubic Lagrange tensor elements on a \(10\times 10\) grid were used. Solutions are shown below.

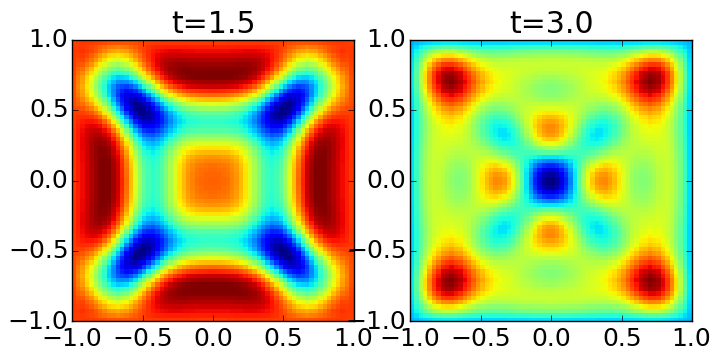
\(E_z\) computed with serendipity polynomial order 1 on grid \(32\times 32\) grid [s11] at \(t=1.5\) (left) and \(t=3.0\) (right).

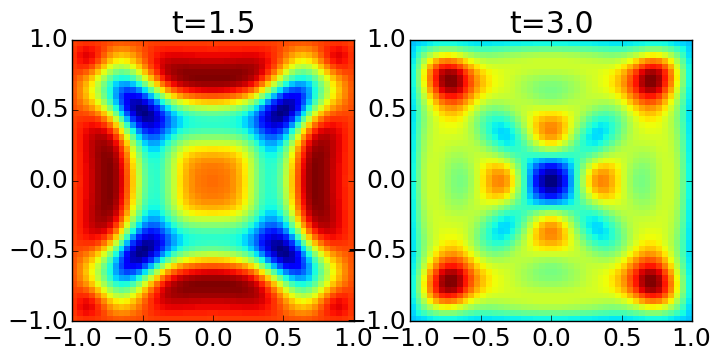
\(E_z\) computed with serendipity polynomial order 2 on grid \(16\times 16\) grid [s12] at \(t=1.5\) (left) and \(t=3.0\) (right).

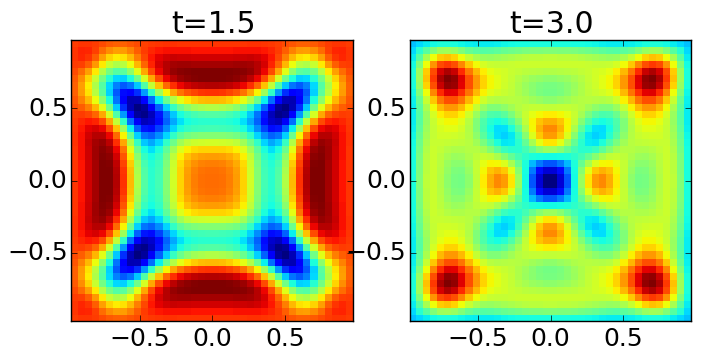
\(E_z\) computed with Lagrange tensor polynomial order 3 on grid \(10\times 10\) grid [s13] at \(t=1.5\) (left) and \(t=3.0\) (right).

As before, the polynomial order 2 solution on half the number of cells in each direction is of comparable quality as the polynomial order 1 solution, and runs about twice as fast.

Conclusion

The nodal DG scheme for 1D and 2D Maxwell equations has been benchmarked. The scheme also works in 3D, however, I have not yet done convergence tests in 3D. The cell averages of the solution converge super-linearly. In general, it appears that using a higher-order method on a coarser grid yields higher quality solution than low-order method on a fine grid. However, this statement is qualitative, and it is not clear what is the “ideal” order and resolution. That requires further study.

I believe that these initial benchmarks give us enough confidence to use the nodal DG updater to evolve the Maxwell equations for the Vlasov-Maxwell and multi-fluid systems.