JE13: 2D Incompressible Euler Solver

Contents

• JE13: 2D Incompressible Euler Solver

  • Problem 1: A double shear flow

  • Problem 2: The Vortex Waltz

    • Second order scheme

    • Third order scheme

  • Conclusions

The 2D incompressible Euler equations can be written in vorticity-streamfunction form

\[\frac{\partial \chi}{\partial t} + \nabla\cdot(\mathbf{u}\chi) = 0\]

where \(\chi\) is the fluid vorticity and \(\mathbf{u} = \nabla\psi\times\mathbf{e}_z\) is the fluid velocity. Here \(\psi\) is the streamfunction determined from a Poisson equation

\[\nabla^2 \psi = -\chi.\]

As the flow is incompressible (\(\nabla\cdot\mathbf{u}=0\)) we can rewrite the fluid equation in the form

\[\frac{\partial \chi}{\partial t} + \{\chi,\psi\} = 0\]

where \(\{\chi,\psi\}\) is the Poisson bracket operator defined by

\[\{\chi,\psi\} = \frac{\partial \chi}{\partial x}\frac{\partial \psi}{\partial y} - \frac{\partial \chi}{\partial y}\frac{\partial \psi}{\partial x}.\]

In this entry I use the FE Poisson solver tested in JE11 and combine it with the Poisson bracket algorithm tested in JE12 to solve this set of equations.

Note

As of May 15th 2012 there is a bug in my Poisson solver which feeds in a non-symmetric matrix to PetSc. This causes very small errors in the potential, which, however, greatly magnify the errors in the total energy. In fact, the total energy plots look bizarre although the solution is just fine.

Till this problem is fixed Gkeyll needs to be run with the -pc_type lu command line option to force PetSc to use a direct Poisson solve instead of the iterative solver.

Problem 1: A double shear flow

In this problem the simulation is initialized with two shear layers. The initially planar shear layers are perturbed slightly due to which they roll around each other, forming finer and finer vortex-like features. The initial conditions for this problem are

\[\begin{split}\chi(x,y,0) = \left\{ \begin{array}{1 1} \delta\cos(x) - \frac{1}{\rho}\mathrm{sech}^2((y-\pi/2)/\rho) \quad y\le\pi \\ \delta\cos(x) + \frac{1}{\rho}\mathrm{sech}^2((3\pi/2-y)/\rho) \quad y\gt\pi \end{array} \right.\end{split}\]

For the results show below \(\rho = \pi/15\) and \(\delta = 0.05\) run up to a time of 8 seconds.

In the first set of simulations, an upwind flux was used with different grid sizes and spatial order schemes to compute the solution. The figure below shows the results at the final time from these simulations.

Double shear problem vorticity at \(t=8\) with different grid resolutions and schemes. Upper left, DG2 on \(64\times 64\) grid [s125], upper right DG2 on \(128\times 128\) grid [s126], lower left, DG3 on \(64\times 64\) grid [s127] and lower right, DG3 on \(128\times 128\) grid [s128]. Note the increasing resolution of features as the spatial order and grid resolution is increased.

In the following two figures the energy and enstrophy history as a function of time is shown. Note that these are conserved quantities of the incompressible Euler equations but need not be conserved by the numerical scheme.

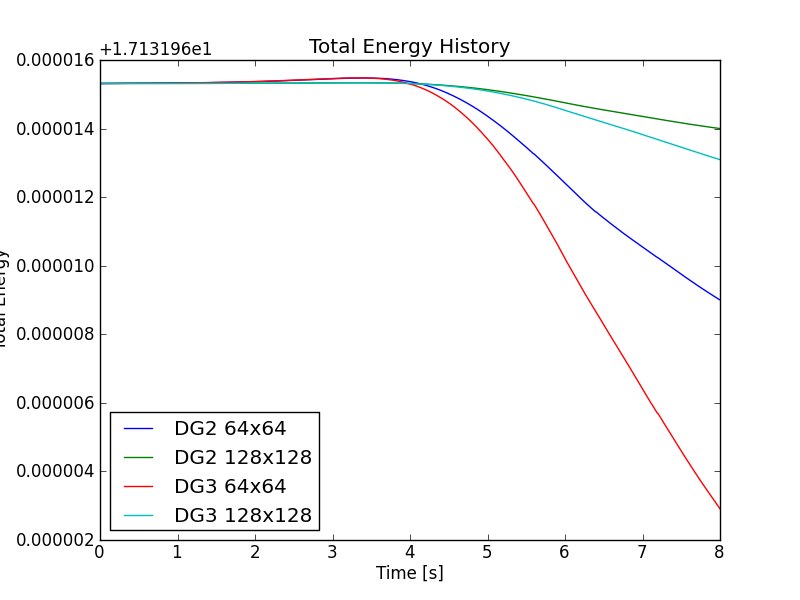
Double shear energy history with different grid resolutions and schemes. Increasing grid resolution reduces the drop in energy, however the spatial order seems to have an opposite effect than expected. I have not figured out why this should be the case and this plot has mystified me.

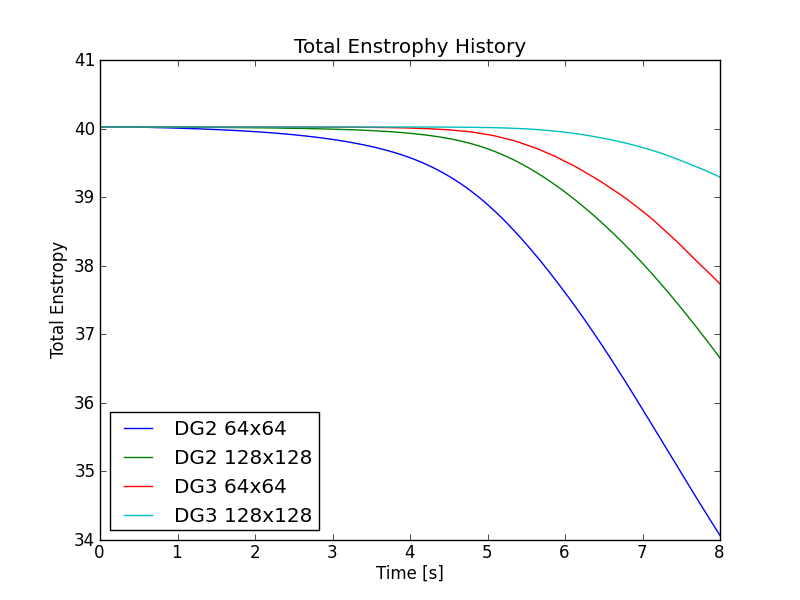
Double shear enstrophy history with different grid resolutions and schemes. Increasing spatial order and grid resolution reduces the drop in enstrophy as expected.

Even with upwind fluxes (used in all the simulations shown above), one can show that the energy is conserved by the spatial discretization exactly. However, in the actual simulations there is a small loss in energy due to the dissipation added from the Runge-Kutta time-stepping and energy conservation proof holds only as \(\Delta t \rightarrow 0\) with the same order as the time integration scheme. This is clearly seen in the plot shown below.

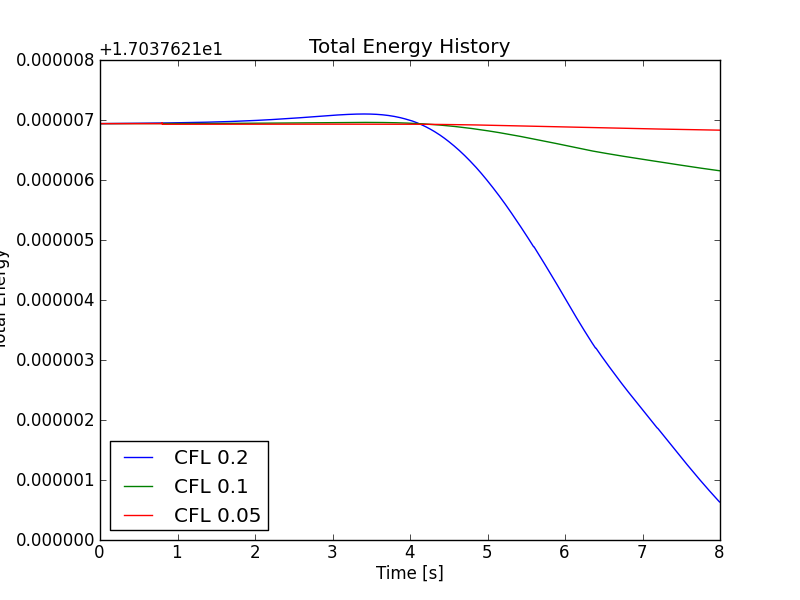
Double shear energy history with DG2 on a \(64\times 64\) grid with different CFL numbers. Blue, CFL 0.2 [s125], green, CFL 0.1 [s129] and red, CFL 0.05 [s130]. The drop in energy is \(6.3\times 10^{-6}\), \(7.8\times 10^{-7}\) and \(1.1\times 10^{-7}\) respectively. This gives energy convergence order of 3.0 and 2.8 respectively.

With central fluxes both energy and enstrophy are conserved to the same order of the time integration scheme. To test this the simulation was run with the second order scheme on a \(64\times 64\) grid with central fluxes and different CFL numbers. The vorticity at \(t=8\) is shown below.

Vorticity at \(t=8\) for double shear problem with central fluxes. Notice the significant phase errors in the solution as compared to the solution with the upwind flux. See [s131] for the input file.

The following figure shows the time history of the energy and enstrophy with central fluxes with different CFL numbers. With reducing time steps the errors in both energy and enstrophy go to zero.

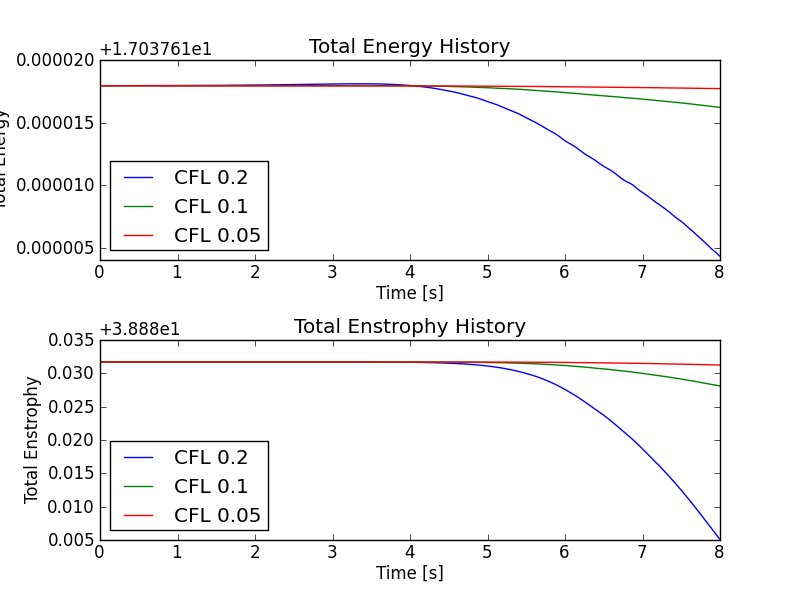
Total energy (top) and total enstrophy (bottom) history with different CFL numbers with central flux. Both energy and enstrophy errors go to zero with the order of time-stepping scheme. The drop in energy is \(1.36\times 10^{-5}\), \(1.73\times 10^{-6}\) and \(2.29\times 10^{-7}\) respectively, giving an order of 2.97 and 2.91 respectively. The drop in enstrophy is \(2.66\times 10^{-2}\), \(3.59\times 10^{-3}\) and \(4.578\times 10^{-4}\) respectively, giving an order of 2.88 and 2.97 respectively. See [s131], [s132] and [s133] for the input files.

Problem 2: The Vortex Waltz

This problem is initialized with two Guassian vortices which merge as they orbit around each other. The vorticity is initialized using the sum of two Gaussians given by

\[\chi(x,y,0) = \omega_1(x,y) + \omega_2(x,y)\]

where

\[\omega_i(x,y) = e^{-r_i^2/0.8}\]

where \(r_i^2 = (x-x_i)^2 + (y-y_i)^2\) and \((x_1,y_1) = (3.5,5.0)\) and \((x_2,y_2) = (6.5,5.0)\).

Second order scheme

The figure below shows the solutions on \(64\times 64\) and \(256\times 256\) grids using the second order scheme with upwind fluxes.

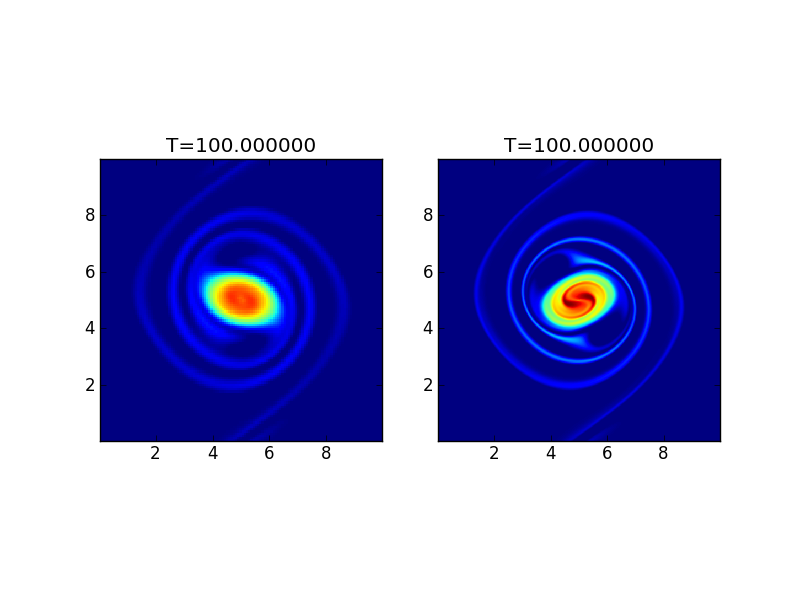
Vorticity for the vortex waltz problem. The left panel shows the solution with \(64 \times 64\) [s134] grid, while the right panel shows the solution with \(256 \times 256\) [s136] grid.

The errors in energy and enstrophy with different grid sizes is shown in the figure below. Note the relatively small drop in energy (on the order of \(10^{-4}\) percent) even for the coarse grid simulation.

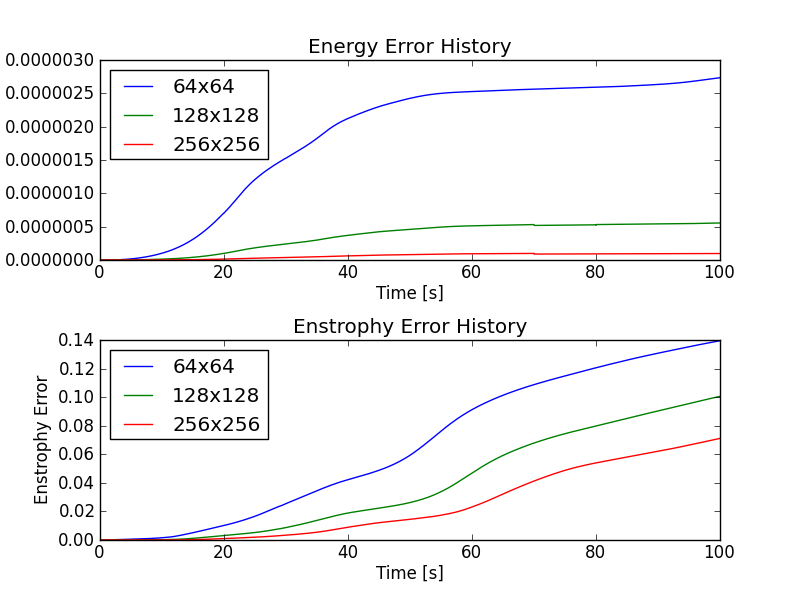
Error in energy (top) and enstrophy (bottom) for the vortex waltz problem with upwind fluxes. The simulations were run on \(64 \times 64\) [s134], \(128 \times 128\) [s135] and \(256 \times 256\) [s136] grids. The error in energy is on the order of \(10^{-4}\) percent even for the coarse grid simulation. Notice that as the upwind flux is used, the enstrophy drop is significant, on the order of 6-14 percent for all the simulations.

To check for conservation (to time-stepping order) of both energy and enstrophy the same simulations were run with a central flux. The results are shown in the following figure. Note that now both energy and enstrophy converge, however, the central flux adds significant numerical noise to the solution.

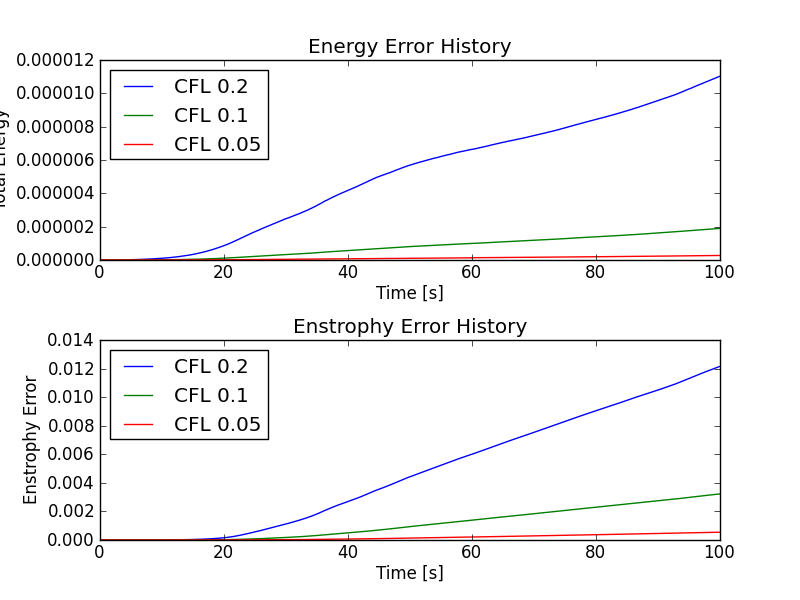
Error in energy (top) and enstrophy (bottom) for the vortex waltz problem with central fluxes. The simulations were run on \(64 \times 64\) grid with CFL numbers of 0.2, 0.1 and 0.05. Energy errors converge with order of 2.53 and 2.97 respectively, while enstrophy errors converge with order of 1.9 and 2.56 respectively. Also, as compared to the case with upwind scheme the error in enstrophy is smaller by more than an order of magnitude. However, this improved enstrophy conservation comes at the cost of adding significant numerical noise to the solution.

Third order scheme

The figure below shows the solutions on \(32\times 32\) and \(64\times 64\) grids using the third order scheme with upwind fluxes.

Vorticity for the vortex waltz problem with the third-order scheme. The left panel shows the solution with \(32 \times 32\) [s137] grid, while the right panel shows the solution with \(64 \times 64\) [s138] grid.

The following figure shows the solution with the third order scheme on \(128\times 128\) grid.

Vorticity for the vortex waltz problem with the third-order scheme on a \(128 \times 128\) [s139] grid. The solution looks better resolved than the \(256 \times 256\) second-order scheme and runs significantly faster.

Conclusions

The Poisson bracket updater combined with the Poisson solver is used to solve the incompressible Euler equations. The results show that energy and enstrophy is conserved (to the order of the time integration scheme) when using a central flux, while the energy is conserved even when using upwind fluxes. It is also shown that the third order spatial scheme is significantly more accurate and runs faster than the second order spatial scheme.