JE17: Solving (Modified) Hasegawa-Wakatani equations

In this note I describe how to solve the Hasegawa-Wakatani system using Gkeyll, both in its original incarnation as well as modified to describe zonal flows.

The Hasegawa-Wakatani system

The Hasegawa-Wakatani (HW) system is a coupled set of equations for the plasma density and electrostatic potential that describe resistive drift wave turbulence. See, for example, the early papers by Hasegawa and Wakatani [Wakatani1986], [Hasegawa1987]. These can be written as

\[\begin{split}\frac{\partial \zeta}{\partial t} + \{\phi,\zeta \} &= \alpha(\phi-n) - \mu \nabla^4\zeta \\ \frac{\partial n}{\partial t} + \{\phi,n \} &= \alpha(\phi-n) - \kappa \frac{\partial \phi}{\partial y} - \mu \nabla^4 n\end{split}\]

where \(\zeta\) is the vorticity, \(\phi\) the electrostatic potential, and \(n\) the perturbed number density. Also, \(\kappa = -\partial/\partial x \ln{n_0}\) is a constant density gradient scale-length, \(\alpha\) is the adiabaticity operator and \(\mu\) is a hyper-diffusion coefficient. Also, \(\{a,b\}\) is the standard canonical Poisson bracket operator. The electrostatic potential itself is determined by solving a Poisson equation

\[\nabla_{\perp}^2\phi = \zeta.\]

Note that in general \(\alpha\) is an operator, coupling the out-of-plane direction, making the system 3D. However, in several important regimes this operator can be replaced by a constant, making the problem 2D. This is the approach taken in this note.

The hyper-diffusive terms are usually added for numerical stability. However, the DG scheme implemented in Gkeyll works fine without these, and hence I have set \(\mu=0\) for all simulations shown here.

The HW system contains two limits that can be obtained by setting \(\alpha=0\) and \(\alpha=\infty\). In the first limit the incompressible hydrodynamic limit is obtained (see JE13 on solving this with Gkeyll). In the second case the Hasegawa-Mima equations are obtained. These can be written as, after identifying \(\phi=n\) and defining \(\zeta'=\zeta-\phi\), as

\[\frac{\partial \zeta'}{\partial t} + \{\phi,\zeta' \} = \kappa \frac{\partial \phi}{\partial y} - \mu \nabla^4 \zeta'\]

with the potential now determined from

\[(\nabla_{\perp}^2-1)\phi = \zeta'\]

As of writing this note, I have not attempted to solve the Hasegawa-Mima equations with Gkeyll, although it should be an easy task.

The modified Hasegawa-Wakatani system

When restricted to 2D the HW system described above does not contain zonal flows. Numata et. al [Numata2007] describe a simple modification that allows capturing zonal flows. This is obtained by observing that in a tokamak edge any potential fluctuations on a flux surface is neutralized by the parallel electron motion. Define the zonal and non-zonal component of any variable \(f\) as

\[\mathrm{zonal:}\ \langle f\rangle \equiv \frac{1}{L_y}\int f dy, \quad \mathrm{nonzonal:}\ \tilde{f} \equiv f - \left<f\right>\]

respectively. Note that in the reduced 2D geometry, the \(y\)-direction is assumed to lie on flux surfaces, while \(x\)-direction is radial. With these definitions, the modified Hasegawa-Wakatani (MHW) equations can be written as

\[\begin{split}\frac{\partial \zeta}{\partial t} + \{\phi,\zeta \} &= \alpha(\tilde{\phi}-\tilde{n}) - \mu \nabla^4\zeta \\ \frac{\partial n}{\partial t} + \{\phi,n \} &= \alpha(\tilde{\phi}-\tilde{n}) - \kappa \frac{\partial \phi}{\partial y} - \mu \nabla^4 n\end{split}\]

These are identical to the standard HW system, except that the adiabatic coupling terms are computed differently.

A note on solving (M)HW systems with Gkeyll

Given the Poisson bracket solver in Gkeyll (see JE12) all that remains to be done is to write a Lua program that combines two of these to update the LHS of the (M)HW system. The drift wave term on the RHS (with \(\kappa\)) is taken into account by including it into the Poisson bracket operator directly. The source term (\(\alpha(\phi-n)\)) is simply accounted for in the Lua script using the accumulate function.

When solving the MHW system the zonal component is computed using a “moment” updater (also used in the Valsov-Poisson solvers) and subtracting it off to compute the nonzonal components needed in the source terms.

The Lua programs are long, but relatively straightforward. See [s215] for an example input file where these are coded up.

In the HW system, with large value of the adiabaticity parameter \(\alpha\) the relaxation time scale from the source term can make the system stiff. In this case I need to use a much smaller time-step than allowed by stability from the Poisson bracket operator alone.

Simulations of the Hasegawa-Wakatani system

In this set of simulations the Hasegawa-Wakatani system was initialized with a Gaussian initial number density profile.

\[n(x,0) = e^{-(x^2+y^2)/s^2}\]

with \(s=2.0\). The initial electrostatic potential was set to \(\phi(x,0)=n(x,0)\) from which \(\zeta(x,0) = \nabla^2_\perp \phi(x,0)\). Simulations were performed for \(\alpha=0.1, 0.3, 1.0, 2.0\). The simulations were run on a \(128\times 128\) grid using piecewise quadratic basis functions.

Note that for \(\alpha=2.0\) the time-scale of relaxation of the potential and number density are much faster than the time-scale from \(E\times B\) advection, which indicates that solutions will be close to those obtained from the Hasegawa-Mima system. Also, I set \(\kappa=1.0\) which provides a free-energy source for the turbulence from the background number density gradient.

Comparisons (with different adiabaticity parameter) for the vorticity, potential and number density are shown below. The initial Gaussian profiles undergo linear drift-wave instabilities which are eventually taken over by nonlinear effects. Once the simulation becomes nonlinear vortices are generated, driving the system into a turbulent state.

With increasing adiabaticity differences in the structure of the generated turbulence are clearly visible. In particular, for \(\alpha=2.0\) the number density and the potential are almost identical, indicating that this regime is that of the Hasegawa-Mima system. The vortex structures smear out with increasing adiabaticity.

Note

As of writing this, I have not performed any statistical analysis of the simulations. However, it is clear that the turbulence is in a saturated state. One way to see this is to monitor the time-step as the simulation progresses. This effectively tracks the \(E\times B\) velocity. In all the results presented below the early on the time-step fluctuates rapidly, settling down a nearly constant value late in the simulation.

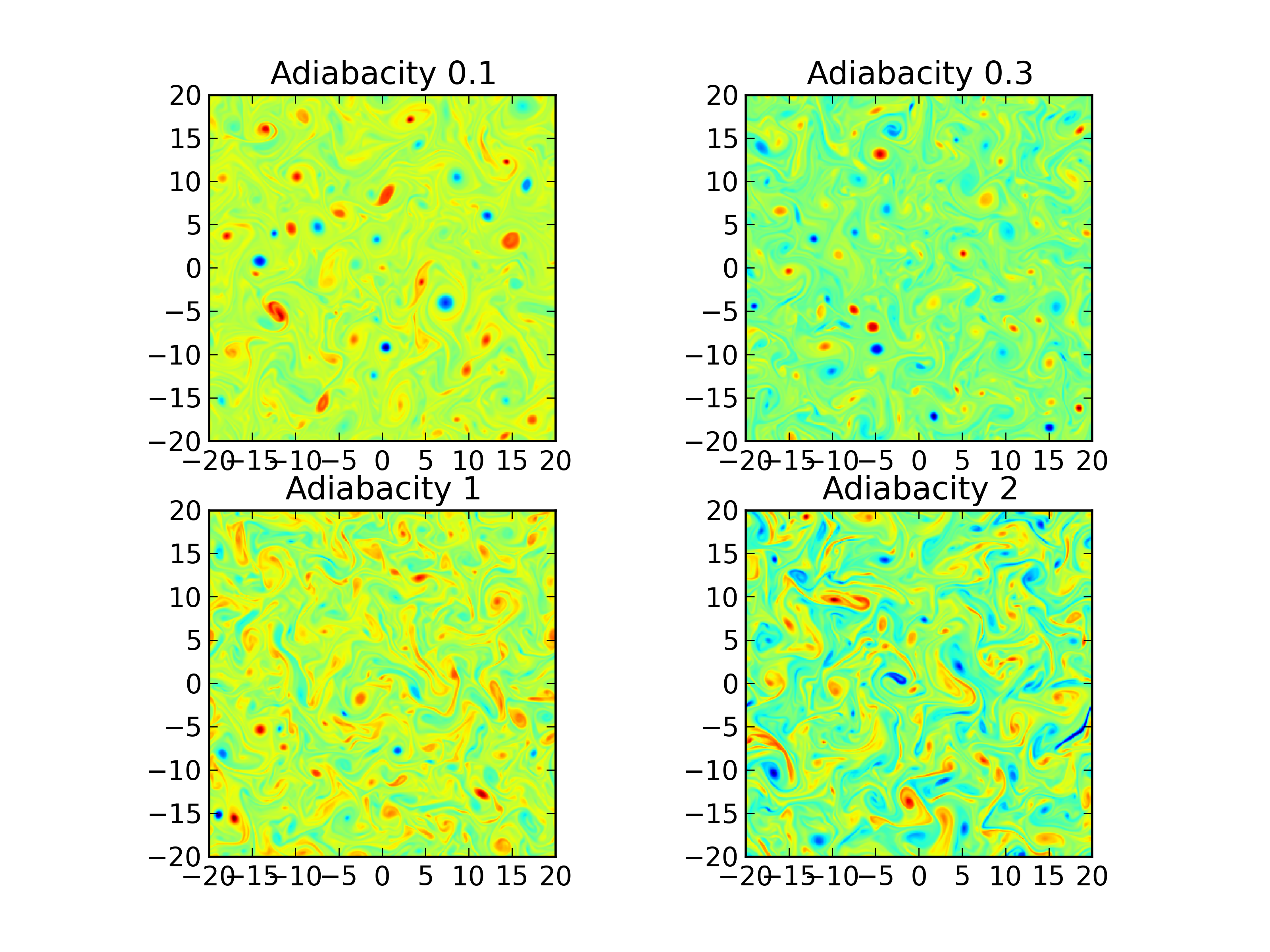
../../_images/hw-cmp-chi_219.png

Comparison of vorticity (\(\zeta\)) with adiabaticity parameter 0.1 (top-left) [s215], 0.3 (top-right) s217], 1.0 (bottom-left) [s215] and 2.0 (bottom-right) [s215] at \(t=200\).

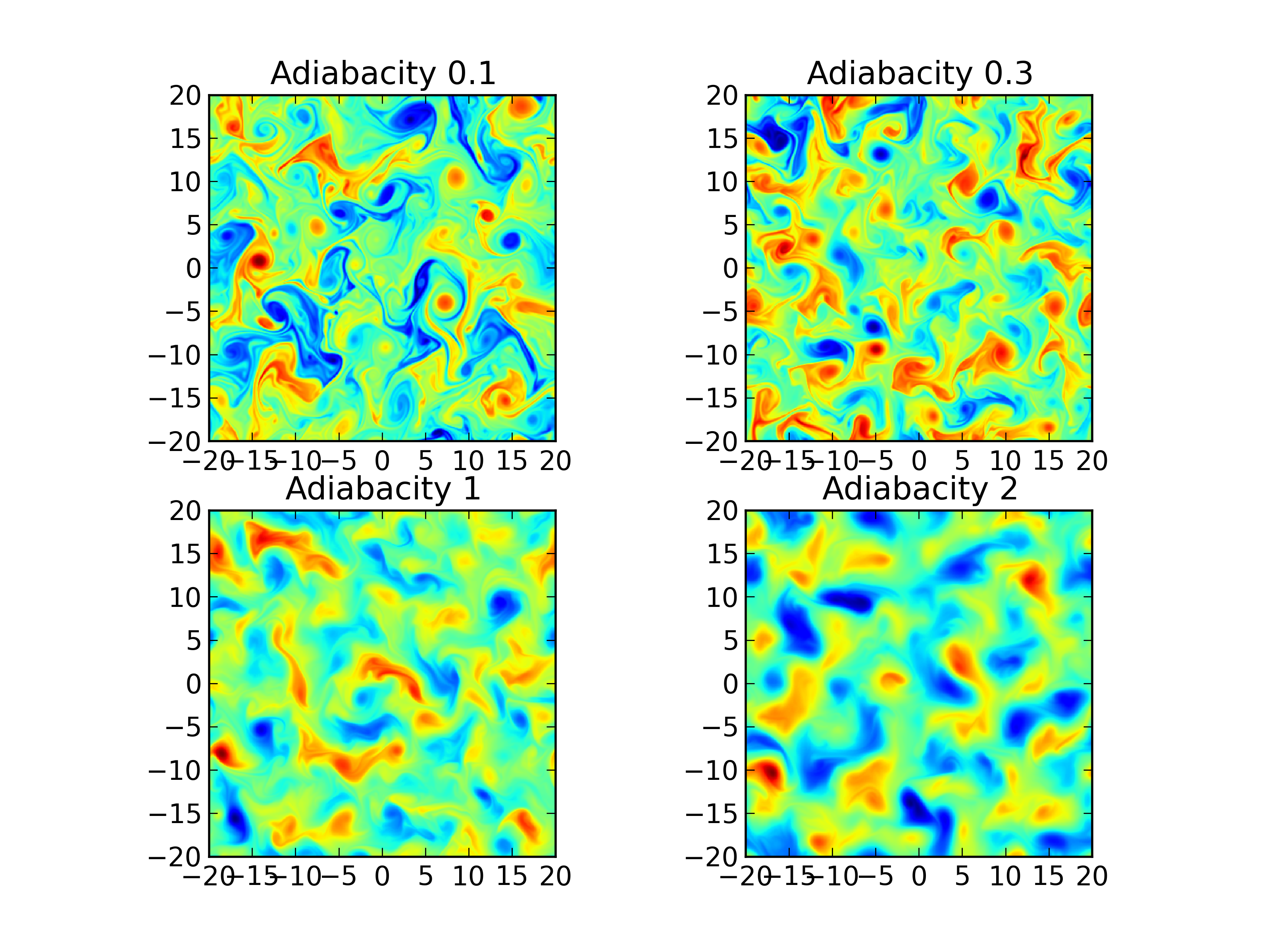
../../_images/hw-cmp-numDens_219.png

Comparison of number density (\(n\)) with adiabaticity parameter 0.1 (top-left) [s215], 0.3 (top-right) [s217], 1.0 (bottom-left) [s215] and 2.0 (bottom-right) [s215] at \(t=200\).

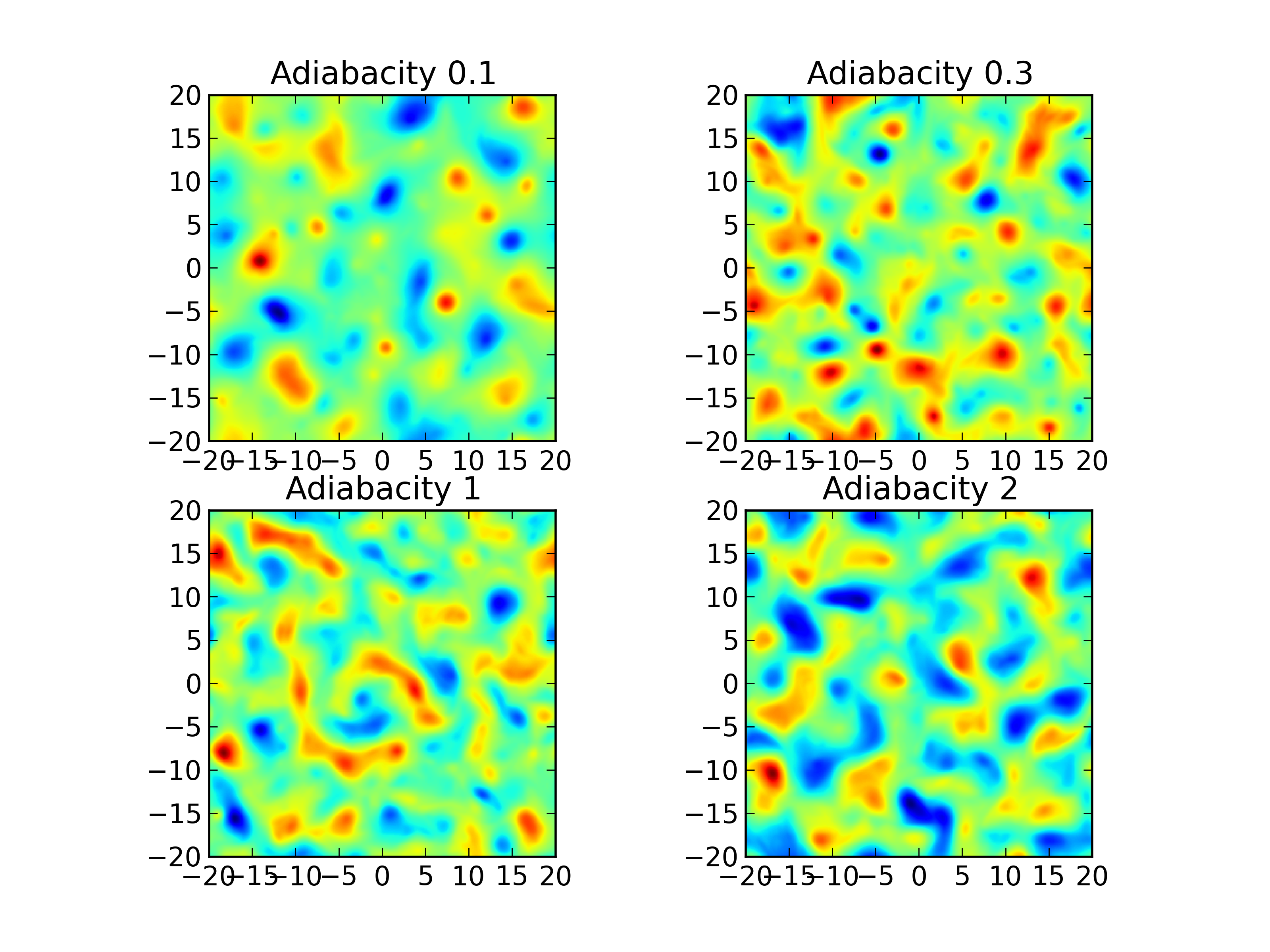
../../_images/hw-cmp-phi_219.png

Comparison of potential (\(\phi\)) with adiabaticity parameter 0.1 (top-left) [s215], 0.3 (top-right) [s217], 1.0 (bottom-left) [s215] and 2.0 (bottom-right) [s215] at \(t=200\).

Simulations of the modified Hasegawa-Wakatani system

For the MHW system, the simulations were initialized with random noise for \(\zeta(x,0)\) and \(n(x,0)\). Poisson equation is solved to determine \(\phi(x,0)\). Adiabaticity parameters of \(\alpha=0.5\) and \(\alpha=1.0\) were used, with \(\kappa=1.0\).

Vortices rapidly form and the solution goes turbulent, initially showing similar vortex patterns as in the unmodified HW system. However, zonal flows soon set in and the turbulent fluctuations in the electrostatic potential are suppressed. The \(y\)-direction gradients in the potential are almost zero, making the \(E\times B\) velocity nearly parallel to the \(y\)-direction.

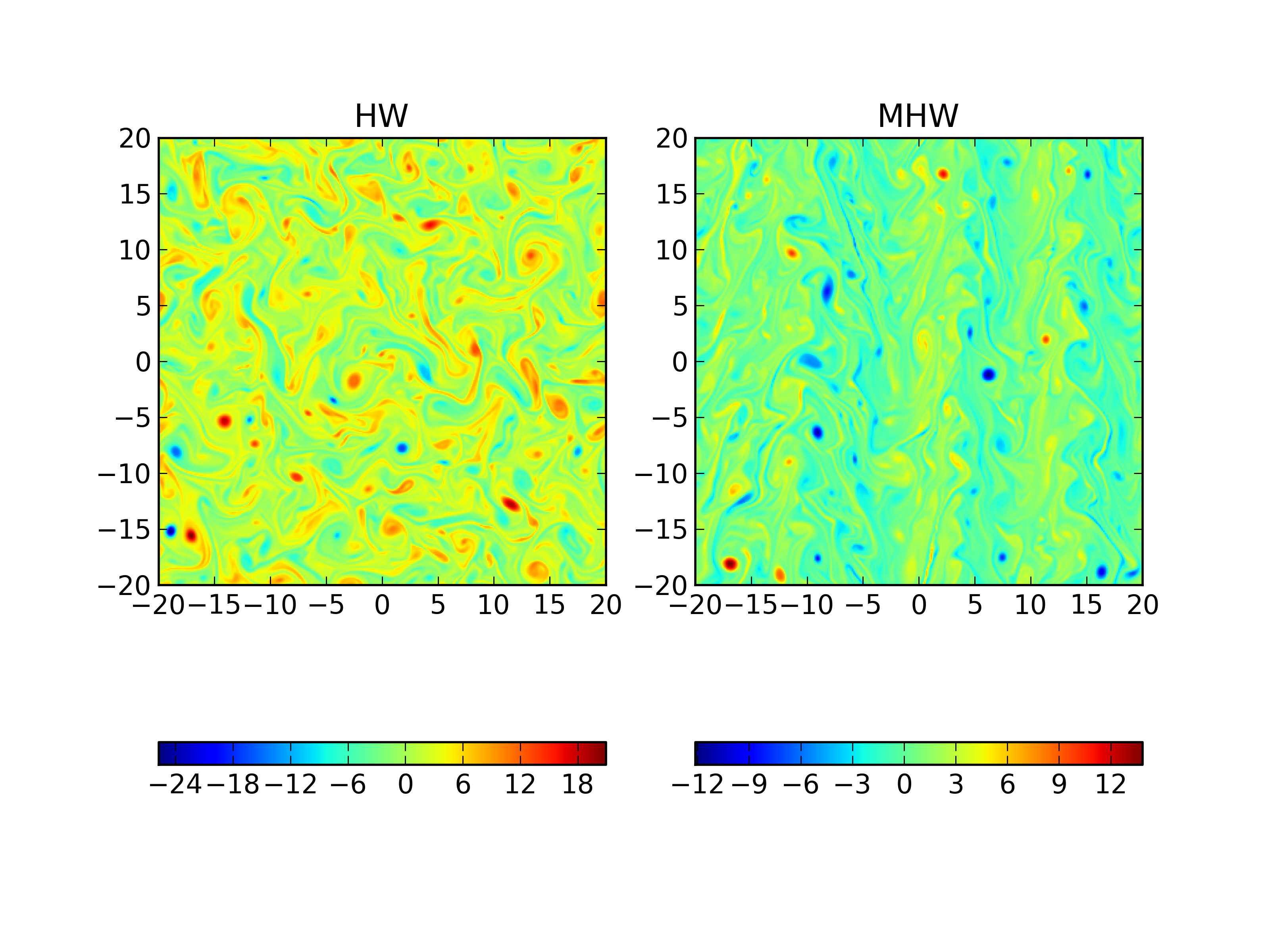
../../_images/mhw-cmp-chi_222.png

Comparison of vorticity (\(\zeta\)) with adiabaticity parameter 1.0 with Hasegawa-Wakatani (left) [s215] and modified Hasegawa-Wakatani [s215] at \(t=200\). Not only is the structure of the fluctuations different, the magnitudes are smaller in the MHW case.

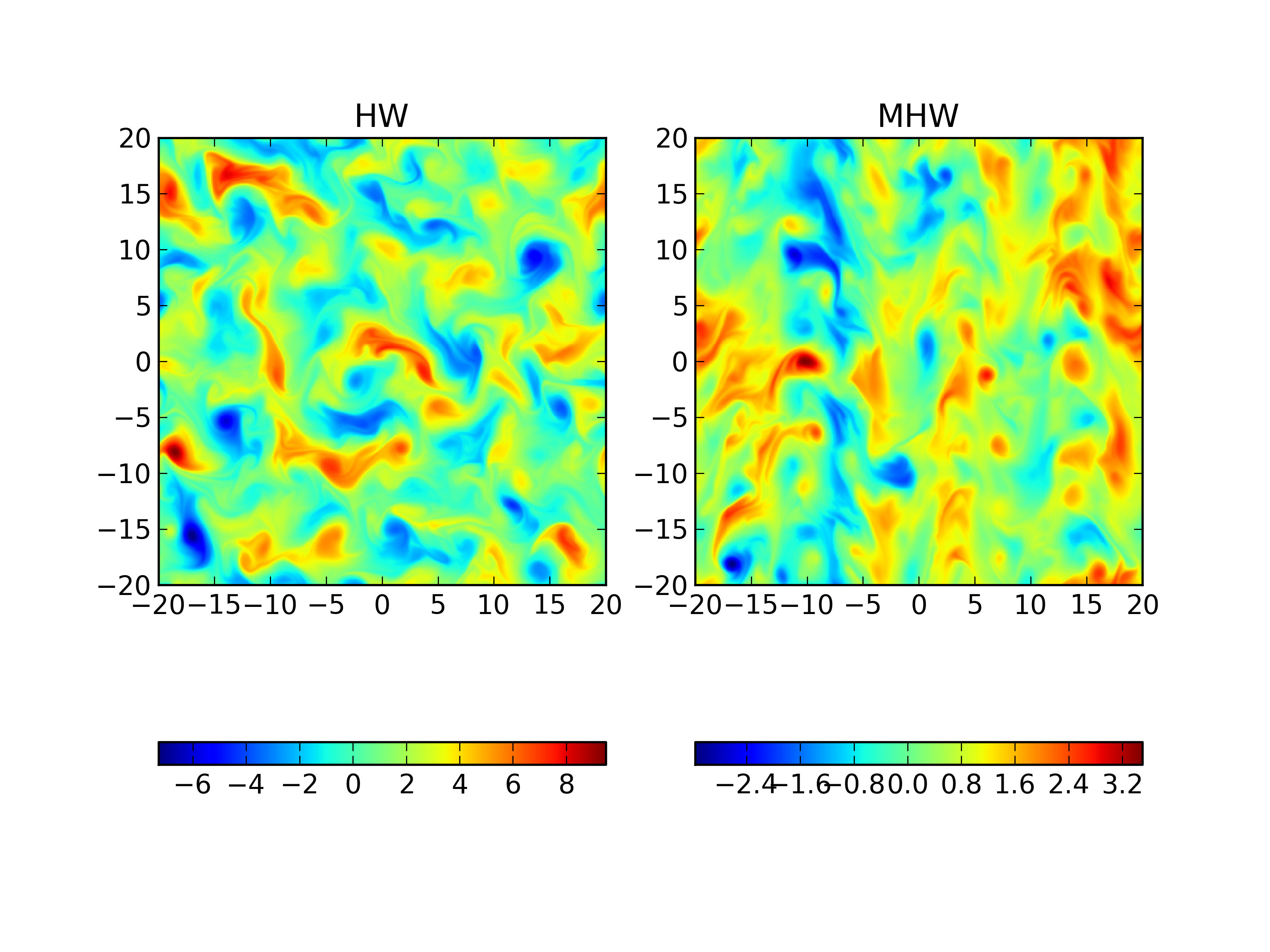
../../_images/mhw-cmp-numDens_222.png

Comparison of number density (\(n\)) with adiabaticity parameter 1.0 with Hasegawa-Wakatani (left) [s215] and modified Hasegawa-Wakatani [s215] at \(t=200\). Not only is the structure of the fluctuations different, the magnitudes are smaller in the MHW case.

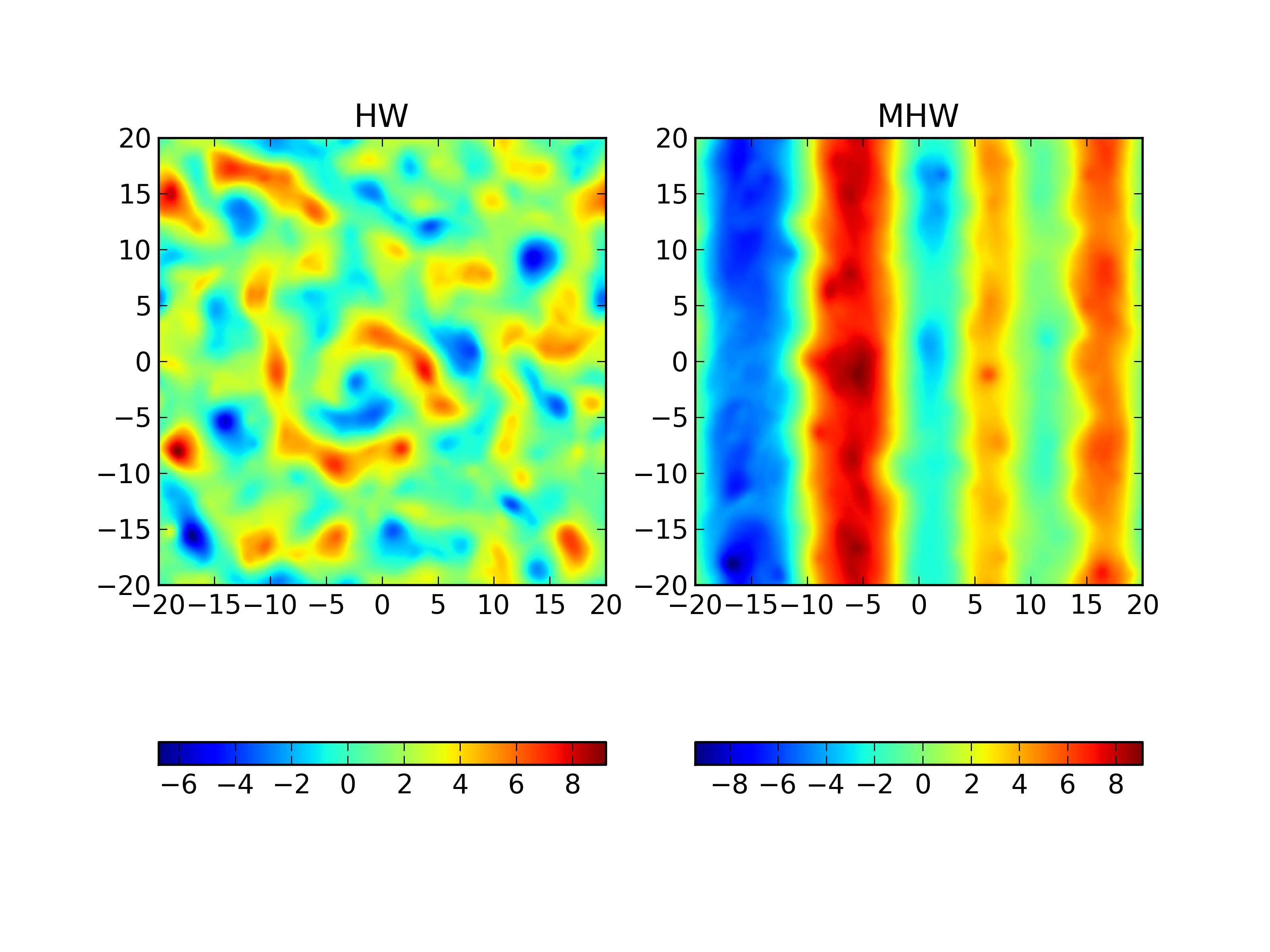
../../_images/mhw-cmp-phi_222.png

Comparison of of potential (\(\phi\)) with adiabaticity parameter 1.0 with Hasegawa-Wakatani (left) [s215] and modified Hasegawa-Wakatani [s215] at \(t=200\). Unlike the vorticity and the number density, the magnitude of the potential are similar. However, the structure is completely different, the turbulence suppressed in the MHW case.

References

Wakatani1986

Masahiro Wakatani and Akira Hasegawa, “A collisional drift wave description of plasma edge turbulence”, Physics of Fluids, 27 (3), 1984.

Hasegawa1987

Akira Hasegawa and Masahiro Wakatani, “Self-Organization of Electrostatic Turbulence in a Cylindrical Plasma”, Physical Review Letters, 59 (14), 1987.

Numata2007

Numata, R., Ball, R., & Dewar, R. L, “Bifurcation in electrostatic resistive drift wave turbulence”. Physics of Plasmas, 14 (10), 102312, 2007.